题目内容
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且 .
.
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入﹣年总成本)
【答案】(1) ;(2)当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.
;(2)当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.
【解析】试题分析:本题考查的知识点是分段函数及函数的最值,分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:分段函数的定义域、值域是各段上x、y取值范围的并集,分段函数的奇偶性、单调性要在各段上分别论证;分段函数的最大值,是各段上最大值中的最大者.第一问,由年利润W=年产量x×每千件的销售收入为R(x)﹣成本,又由 ,且年固定成本为10万元,每生产1千件需另投入2.7万元.我们易得年利润W(万元)关于年产量x(千件)的函数解析式;
,且年固定成本为10万元,每生产1千件需另投入2.7万元.我们易得年利润W(万元)关于年产量x(千件)的函数解析式;
第二问,由第一问的解析式,我们求出各段上的最大值,即利润的最大值,然后根据分段函数的最大值是各段上最大值的最大者,即可得到结果.
试题解析:(1)当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
∴ .
.
(2)①当![]() 时,由
时,由![]() ,得
,得![]() ,
,
且当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
∴当![]() 时,W取最大值,且
时,W取最大值,且![]() ,
,
②当![]() 时,
时, ![]() ,
,
当且仅当![]() ,
,
即![]() 时,
时, ![]() ,
,
故当![]() 时,W取最大值38.
时,W取最大值38.
综合①②知当![]() 时,W取最大值38.6万元,故当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.
时,W取最大值38.6万元,故当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.

 走进文言文系列答案
走进文言文系列答案【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: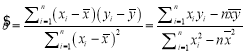 ,
,![]() .
.