题目内容
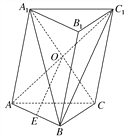
【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)利用线面平行的判定定理,通过中位线平行得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ;(2)要证明
;(2)要证明![]() 线线垂直,则证明
线线垂直,则证明![]() 平面
平面![]() 线面垂直,所以根据线面垂直的判定定理,找到
线面垂直,所以根据线面垂直的判定定理,找到![]() ,则得证。
,则得证。
试题解析:
(1)连接BC1,因为侧面AA1C1C是菱形,AC1与A1C交于点O,所以O为AC1的中点,又因为E是AB的中点,所以OE∥BC1,因为OE平面BCC1B1,BC1平面BCC1B1,所以OE∥平面BCC1B1.
(2)因为侧面AA1C1C是菱形,所以AC1⊥A1C,因为AC1⊥A1B,A1C∩A1B=A1,A1C平面A1BC,A1B平面A1BC,所以AC1⊥平面A1BC,因为BC平面A1BC,所以AC1⊥BC.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

