题目内容
【题目】已知函数f(x)=lnx+(e﹣a)x﹣b,其中e为自然对数的底数.若不等式f(x)≤0恒成立,则 ![]() 的最小值为 .
的最小值为 .
【答案】﹣ ![]()
【解析】解:∵函数f(x)=lnx+(e﹣a)x﹣b,其中e为自然对数的底数, ∴ ![]() ,x>0,
,x>0,
当a≤e时,f′(x)>0,
f(x)在(0,+∞)上是增函数,∴f(x)≤0不可能恒成立,
当a>e时,由 ![]() ,得x=
,得x= ![]() ,
,
∵不等式f(x)≤0恒成立,∴f(x)的最大值为0,
当x∈(0, ![]() )时,f′(x)>0,f(x)单调递增,
)时,f′(x)>0,f(x)单调递增,
当x∈( ![]() ,+∞)时,f′(x)<0,f(x)单调递减,
,+∞)时,f′(x)<0,f(x)单调递减,
∴当x= ![]() 时,f(x)取最大值,
时,f(x)取最大值,
f( ![]() )=﹣ln(a﹣e)﹣b﹣1≤0,
)=﹣ln(a﹣e)﹣b﹣1≤0,
∴ln(a﹣e)+b+1≥0,
∴b≥﹣1﹣ln(a﹣e),
∴ ![]() (a>e),
(a>e),
令F(x)= ![]() ,x>e,
,x>e,
F′(x)= 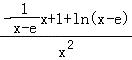 =
= ![]() ,
,
令H(x)=(x﹣e)ln(x﹣e)﹣e,
H′(x)=ln(x﹣e)+1,
由H′(x)=0,得x=e+ ![]() ,
,
当x∈(e+ ![]() ,+∞)时,H′(x)>0,H(x)是增函数,
,+∞)时,H′(x)>0,H(x)是增函数,
x∈(e,e+ ![]() )时,H′(x)<0,H(x)是减函数,
)时,H′(x)<0,H(x)是减函数,
∴当x=e+ ![]() 时,H(x)取最小值H(e+
时,H(x)取最小值H(e+ ![]() )=﹣e﹣
)=﹣e﹣ ![]() ,
,
∵x→e时,H(x)→0,x>2e时,H(x)>0,H(2e)=0,
∴当x∈(e,2e)时,F′(x)<0,F(x)是减函数,
当x∈(2e,+∞)时,F′(x)>0,F(x)是增函九,
∴x=2e时,F(x)取最小值,F(2e)= ![]() =﹣
=﹣ ![]() ,
,
∴ ![]() 的最小值为﹣
的最小值为﹣ ![]() .
.
故答案为:﹣ ![]() .
.
求出 ![]() ,x>0,当a≤e时,f′(x)>0,f(x)≤0不可能恒成立,当a>e时,由
,x>0,当a≤e时,f′(x)>0,f(x)≤0不可能恒成立,当a>e时,由 ![]() ,得x=
,得x= ![]() ,由题意当x=
,由题意当x= ![]() 时,f(x)取最大值0,推导出
时,f(x)取最大值0,推导出 ![]() (a>e),令F(x)=
(a>e),令F(x)= ![]() ,x>e,F′(x)=
,x>e,F′(x)= ![]() ,令H(x)=(x﹣e)ln(x﹣e)﹣e,H′(x)=ln(x﹣e)+1,由此利用导数性质能求出
,令H(x)=(x﹣e)ln(x﹣e)﹣e,H′(x)=ln(x﹣e)+1,由此利用导数性质能求出 ![]() 的最小值.
的最小值.