Question

【题目】给定数列{cn}，如果存在常数p、q使得cn+1＝pcn+q对任意n∈N*都成立，则称{cn}为“M类数列”．

（1）若{an}是公差为d的等差数列，判断{an}是否为“M类数列”，并说明理由；

（2）若{an}是“M类数列”且满足：a1＝2，an+an+1＝32n．

①求a2、a3的值及{an}的通项公式；

②设数列{bn}满足：对任意的正整数n，都有a1bn+a2bn﹣1+a3bn﹣2+…+anb1＝32n+1﹣4n﹣6，且集合M＝{n|≥λ，n∈N*}中有且仅有3个元素，试求实数λ的取值范围．

Answer 1

【答案】（1）见解析；（2）① ，；②

【解析】

（1）通过an+1＝an+d与cn+1＝pcn+q比较可知p＝1、q＝d，进而可得结论；

（2）①通过a1＝2、an+an+1＝32n计算出a2、a3的值，进而利用数列{an}是“M类数列”代入计算可知数列{an}是以首项、公比均为2的等比数列，计算可得结论；②通过①可知2bn+22bn﹣1+23bn﹣2+…+2nb1＝32n+1﹣4n﹣6，利用2bn＝（2bn+22bn﹣1+23bn﹣2+…+2nb1）﹣（22bn﹣1+23bn﹣2+…+2nb1）计算可知bn＝2n﹣1，从而M＝{n|≥λ，n∈N*}，分别计算出当n＝1、2、3时λ的值，进而可得结论．

（1）结论：公差为d的等差数列是“M类数列”．理由如下：

∵数列{an}是公差为d的等差数列，∴an+1＝an+d，此时p＝1、q＝d，

即公差为d的等差数列是“M类数列”；

（2）①∵a1＝2，an+an+1＝32n，∴a2＝32﹣a1＝4，，

又∵数列{an}是“M类数列”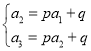，∴，即，解得：p＝2，q＝0，

即an+1＝2an，又∵a1＝2，∴数列{an}是以首项、公比均为2的等比数列，

∴数列{an}的通项公式an＝2n；

②由①可知a1bn+a2bn﹣1+a3bn﹣2+…+anb1＝32n+1﹣4n﹣6，

即2bn+22bn﹣1+23bn﹣2+…+2nb1＝32n+1﹣4n﹣6，

∴2bn﹣1+22bn﹣2+23bn﹣3+…+2n﹣1b1＝32n﹣4（n﹣1）﹣6＝32n﹣4n﹣2，

∴22bn﹣1+23bn﹣2+…+2nb1＝32n+1﹣8n﹣4，

∴2bn＝（2bn+22bn﹣1+23bn﹣2+…+2nb1）﹣（22bn﹣1+23bn﹣2+…+2nb1）

＝（32n+1﹣4n﹣6）﹣（32n+1﹣8n﹣4）

＝4n﹣2，

即bn＝2n﹣1，当时，也符合上式，所以bn＝2n﹣1.

∴集合M＝{n|≥λ，n∈N*}＝{n|≥λ，n∈N*}，

当n＝1时，λ≤ ；当n＝2时，λ≤；

当n＝3时，λ≤ ；当n≥4时，λ≤；

又∵集合M＝{n|≥λ，n∈N*}中有且仅有3个元素，∴，

故实数λ的取值范围是．