题目内容
(本题12分)已知数列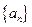 满足
满足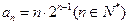 .是否存在等差数列
.是否存在等差数列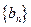 ,使得数列
,使得数列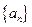 与
与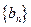 满足
满足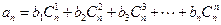 对一切正整数
对一切正整数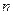 成立? 证明你的结论.
成立? 证明你的结论.
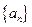 满足
满足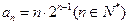 .是否存在等差数列
.是否存在等差数列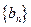 ,使得数列
,使得数列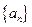 与
与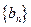 满足
满足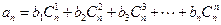 对一切正整数
对一切正整数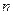 成立? 证明你的结论.
成立? 证明你的结论. A
令 ,有
,有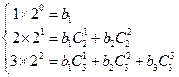 ,即
,即 ,
,
解得 . 由此猜想:
. 由此猜想: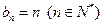 . ----------------4分
. ----------------4分
下面证明: .
.
解法一:设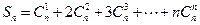
有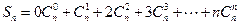
又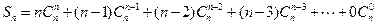 ------------8分
------------8分
两式相加 ------------10分
------------10分
故 ,即
,即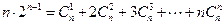 . ------------12分
. ------------12分
解法二:构造函数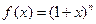 ,
,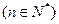 ,由二项式定理,知
,由二项式定理,知
 , -------------------8分
, -------------------8分
对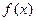 求导,得
求导,得 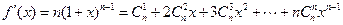 ---10分
---10分
令 ,即得
,即得 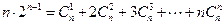 . -------------------12分
. -------------------12分
解法三:⑴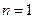 时,
时,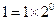 成立. --------------------------5分
成立. --------------------------5分
⑵假设当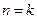 时等式成立,即
时等式成立,即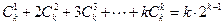 .
.
当 时,
时, 
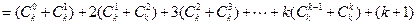
--------------------------------8分
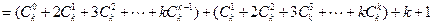


--------------------10分


也就是说,当 时,等式也成立.
时,等式也成立.
由⑴⑵可知,存在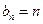 ,使得
,使得 对一切
对一切 成立. ---------------------12分
成立. ---------------------12分
 ,有
,有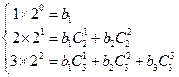 ,即
,即 ,
,解得
 . 由此猜想:
. 由此猜想: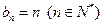 . ----------------4分
. ----------------4分 下面证明:
 .
.解法一:设
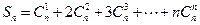
有
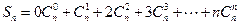
又
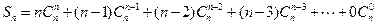 ------------8分
------------8分两式相加
 ------------10分
------------10分故
 ,即
,即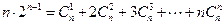 . ------------12分
. ------------12分解法二:构造函数
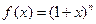 ,
,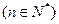 ,由二项式定理,知
,由二项式定理,知 , -------------------8分
, -------------------8分对
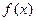 求导,得
求导,得 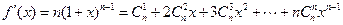 ---10分
---10分令
 ,即得
,即得 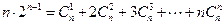 . -------------------12分
. -------------------12分解法三:⑴
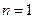 时,
时,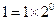 成立. --------------------------5分
成立. --------------------------5分⑵假设当
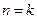 时等式成立,即
时等式成立,即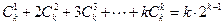 .
.当
 时,
时, 
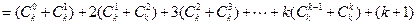
--------------------------------8分
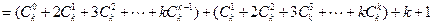


--------------------10分


也就是说,当
 时,等式也成立.
时,等式也成立.由⑴⑵可知,存在
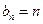 ,使得
,使得 对一切
对一切 成立. ---------------------12分
成立. ---------------------12分
练习册系列答案
相关题目
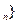 中,a
中,a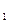 =5且a
=5且a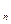 =3a
=3a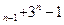 (n≥2)
(n≥2)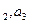 的值.
的值.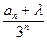 ,是否存在实数λ,使数列{b
,是否存在实数λ,使数列{b )
)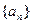 生成的数列
生成的数列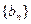 满足对任意的
满足对任意的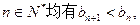 其中
其中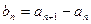 ,则称数列
,则称数列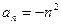 ,试判断数列
,试判断数列 II)若数列
II)若数列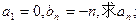
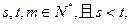 求证
求证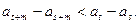
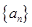 是等差数列,
是等差数列,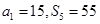 ,则过点
,则过点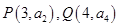 的直线斜率为
的直线斜率为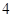
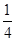
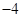
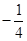
 中,
中, ,前4项和为1111,则该数列的公比为( )
,前4项和为1111,则该数列的公比为( )
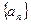 满足
满足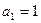 ,
,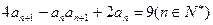
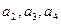 。(2)由(1)猜想
。(2)由(1)猜想 (3)用数学归纳法证明(2)的结果。
(3)用数学归纳法证明(2)的结果。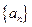 中,
中,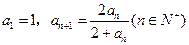 ,则
,则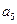 等于______ _.
等于______ _.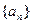 的前n项和为
的前n项和为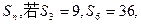 则
则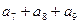 =" " ( )
=" " ( )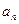 }的首项为
}的首项为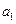 =
=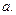 公比为q,则
公比为q,则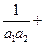
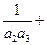 …
…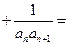 __________。
__________。