题目内容
1.函数y=f(x)的解析式由下列程序确定
根据左侧程序求下列各式的值(直接写出结果即可)
(1)f( $\frac{π}{6}$ )=3;
(2)f(0)=0;
(3)f(-$\frac{1}{2}$)=$\frac{3\sqrt{2}}{2}$;
(4)f[f( $\frac{2π}{3}$ )]=$\frac{1}{4}$+$\sqrt{2}$;
(5)函数f(x)的解析式为:f(x)=$\left\{\begin{array}{l}{\stackrel{sin(x+\frac{π}{3})+4cos2x}{0}}&{\stackrel{x>0}{x=0}}\\{{2}^{x}+\sqrt{2}}&{x<0}\end{array}\right.$.
分析 模拟执行程序,可得程序的功能是求分段函数f(x)=$\left\{\begin{array}{l}{\stackrel{sin(x+\frac{π}{3})+4cos2x}{0}}&{\stackrel{x>0}{x=0}}\\{{2}^{x}+\sqrt{2}}&{x<0}\end{array}\right.$的值,即可得解.
解答 解:∵模拟执行程序,可得程序的功能是求分段函数f(x)=$\left\{\begin{array}{l}{\stackrel{sin(x+\frac{π}{3})+4cos2x}{0}}&{\stackrel{x>0}{x=0}}\\{{2}^{x}+\sqrt{2}}&{x<0}\end{array}\right.$的值,
∴(1)3 (2)0 (3)$\frac{3\sqrt{2}}{2}$ (4)$\frac{1}{4}$+$\sqrt{2}$ (5)f(x)=$\left\{\begin{array}{l}{\stackrel{sin(x+\frac{π}{3})+4cos2x}{0}}&{\stackrel{x>0}{x=0}}\\{{2}^{x}+\sqrt{2}}&{x<0}\end{array}\right.$.
故答案为:3,0,$\frac{3\sqrt{2}}{2}$,$\frac{1}{4}$+$\sqrt{2}$,f(x)=$\left\{\begin{array}{l}{\stackrel{sin(x+\frac{π}{3})+4cos2x}{0}}&{\stackrel{x>0}{x=0}}\\{{2}^{x}+\sqrt{2}}&{x<0}\end{array}\right.$.
点评 本题主要考查了条件语句的伪代码,①IF-THEN-ELSE:执行时,先对IF后的条件进行判断,若条件符合,执行语句1,否则执行语句2.②IF-THEN:执行时,先对IF后的条件进行判断,若条件符合,执行THEN后的语句,否则结束条件语句,属于基础题.

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m⊥α,m?β,则α⊥β | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α |
| A. | l?α,m?α且l∥β,m∥β | B. | l?α,m?β且l∥m | ||
| C. | l⊥α,m⊥β且l∥m | D. | l∥α,m∥β且l∥m |
| A. | 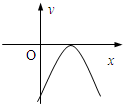 | B. | 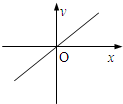 | C. | 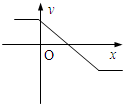 | D. | 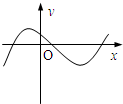 |