题目内容
6.m,n,l是直线,α,β是两个不同的平面,下面说法正确的是( )| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m⊥α,m?β,则α⊥β | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α |
分析 在A中,α与β相交或平行;在B中,由平面与平面垂直的判定定理得α⊥β;在C中,n与α相交或n∥α;在D中,只有当m与n相交时,才有l⊥α.
解答 解:若m∥α,m∥β,则α与β相交或平行,故A错误;
若m⊥α,m?β,则由平面与平面垂直的判定定理得α⊥β,故B正确;
若m?α,n?α,m,n是异面直线,则n与α相交或n∥α,故C错误;
若m?α,n?α,l⊥m,l⊥n,则只有当m与n相交时,才有l⊥α,故D错误.
故选:B.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
17.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得$\sqrt{{a_m}{a_n}}=32{a_1}$,则$\frac{1}{m}$+$\frac{4}{n}$的最小值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
14.已知$\overrightarrow{a}$=(2,0,2),$\overrightarrow{b}$=(-1,-1,0),则错误的是( )
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | <$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{2π}{3}$ | ||
| C. | $\overrightarrow{a}$在$\overrightarrow{b}$上的射影为-$\sqrt{2}$ | D. | $\overrightarrow{b}$在$\overrightarrow{a}$上的射影为-$\frac{\sqrt{2}}{2}$ |
11.已知定义在R上函数f(x)部分自变量与函数值对应关系如表,若f(x)为偶函数,且在[0,+∞)上为增函数,不等式1<f(x-1)<2的解集是( )
| x | 0 | 2 | 3 | 4 |
| f(x) | -1 | 1 | 2 | 3 |
| A. | (-2,-1) | B. | (3,4) | C. | (-2,-1)∪(3,4) | D. | (-2,4) |
16.设p:x≥0,q:log${\;}_{\frac{1}{2}}$(x+1)>0,则¬p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分敢不必要条件 |

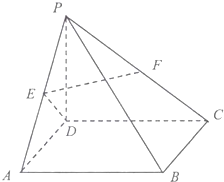 如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.