题目内容
已知函数f (x)=f (p-x),且当 时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )
时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )
 时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )
时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )| A.a<b<c | B.b<c<a | C.c<b<a | D.c<a<b |
D
解:∵函数y=f(x)满足f(x)=f(π-x),
∴函数y=f(x)的图象关于直线x=π 2 对称,
因为当 x∈(0,π/ 2 )时,f(x)=x+sinx,
所以f′(x)=1+cosx>0在(0,π/ 2 )上恒成立,
所以函数在(0,π/2 )上是增函数,
所以函数y=f(x)在( π /2 ,π )上是减函数.
因为2距离对称轴最近,其次是1,最远的时3,
所以根据函数的有关性质可得:f(3)<f(1)<f(2),即 c<a<b,
故选D.
∴函数y=f(x)的图象关于直线x=π 2 对称,
因为当 x∈(0,π/ 2 )时,f(x)=x+sinx,
所以f′(x)=1+cosx>0在(0,π/ 2 )上恒成立,
所以函数在(0,π/2 )上是增函数,
所以函数y=f(x)在( π /2 ,π )上是减函数.
因为2距离对称轴最近,其次是1,最远的时3,
所以根据函数的有关性质可得:f(3)<f(1)<f(2),即 c<a<b,
故选D.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
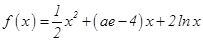 ,
, (其中
(其中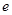 为自然对数的底数,常数
为自然对数的底数,常数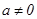 ).
).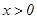 ,
,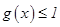 恒成立,求正实数
恒成立,求正实数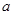 的取值范围;
的取值范围;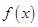 在区间
在区间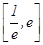 上的单调性;
上的单调性;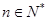 ,不等式
,不等式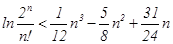 成立.
成立.  (不含锥形盖内空间),盖子的母线与底面圆半径的夹角为
(不含锥形盖内空间),盖子的母线与底面圆半径的夹角为 ,设粮囤的底面圆半径为R
,设粮囤的底面圆半径为R ,需用白铁皮的面积记为
,需用白铁皮的面积记为 (不计接头等)。
(不计接头等)。 表示为R的函数;
表示为R的函数;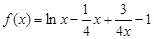 .
.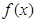 的单调区间;
的单调区间;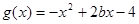 ,若对任意
,若对任意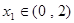 ,
,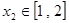 ,不等式
,不等式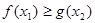 恒成立,求实数
恒成立,求实数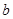 的取值范围.
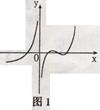
的取值范围.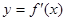 的图象可能为( )
的图象可能为( )

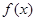 在
在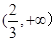 上存在单调递增区间,求
上存在单调递增区间,求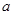 的取值范围;
的取值范围;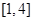 上的最值.
上的最值.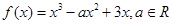
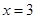 是
是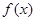 的极值点,求
的极值点,求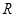 上的单调递增函数,求实数
上的单调递增函数,求实数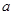 的取值范围.
的取值范围.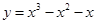 的单调递减区间是 。
的单调递减区间是 。