题目内容
设
(1)若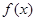 在
在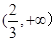 上存在单调递增区间,求
上存在单调递增区间,求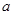 的取值范围;
的取值范围;
(2)当a=1时,求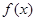 在
在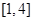 上的最值.
上的最值.

(1)若
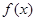 在
在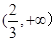 上存在单调递增区间,求
上存在单调递增区间,求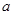 的取值范围;
的取值范围;(2)当a=1时,求
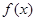 在
在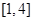 上的最值.
上的最值. (1)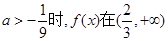 上存在单调递增区间
上存在单调递增区间
(2)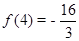
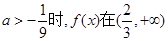 上存在单调递增区间
上存在单调递增区间(2)
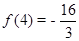
(1)题目转化为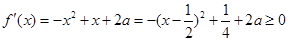 在
在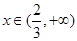 上有解。进而转化为
上有解。进而转化为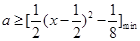 即可.
即可.
(2)利用导数求其极值,然后与区间的端点的函数值比较,最大的就是最大值,最小的就是最小值。
解:(1)由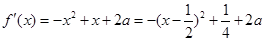 --------2分
--------2分
当
令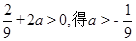
所以,当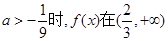 上存在单调递增区间 --------4分
上存在单调递增区间 --------4分
(2)当a=1时,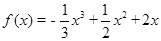
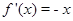 2+x+2,令
2+x+2,令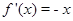 2+x+2=0得x1=-1,x2=2------------6分
2+x+2=0得x1=-1,x2=2------------6分
因为 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
所以在[1,4]上的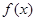 在[1,4]上的最大值为
在[1,4]上的最大值为
因为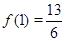 ,
,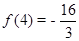 最小值为
最小值为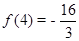
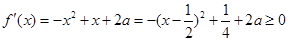 在
在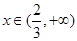 上有解。进而转化为
上有解。进而转化为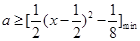 即可.
即可.(2)利用导数求其极值,然后与区间的端点的函数值比较,最大的就是最大值,最小的就是最小值。
解:(1)由
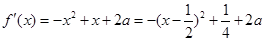 --------2分
--------2分当

令
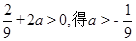
所以,当
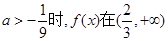 上存在单调递增区间 --------4分
上存在单调递增区间 --------4分(2)当a=1时,
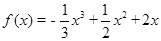
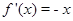 2+x+2,令
2+x+2,令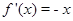 2+x+2=0得x1=-1,x2=2------------6分
2+x+2=0得x1=-1,x2=2------------6分因为
 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.所以在[1,4]上的
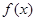 在[1,4]上的最大值为
在[1,4]上的最大值为
因为
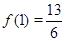 ,
,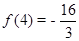 最小值为
最小值为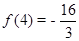

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
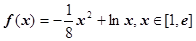
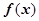 的单调区间;(Ⅱ)求
的单调区间;(Ⅱ)求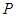 从点
从点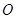 出发,按逆时针方向沿周长为
出发,按逆时针方向沿周长为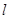 的图形运动一周,
的图形运动一周,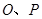 两点连线的距离
两点连线的距离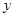 与点
与点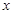 的函数关系如图,那么点
的函数关系如图,那么点
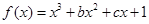 有两个极值点
有两个极值点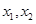 且
且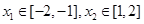 ,则
,则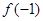 的取值范围是( )
的取值范围是( )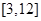
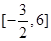
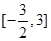
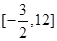
 时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )
时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )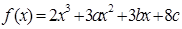 在
在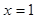 及
及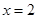 时取得极值.
时取得极值.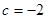 时,求函数
时,求函数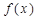 在区间
在区间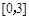 上的最大值.
上的最大值. 的图像如左图所示,那么函数
的图像如左图所示,那么函数 的图像最有可能的是( )
的图像最有可能的是( )
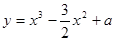 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________ 在点(0,1)处的切线方程为 ▲ .
在点(0,1)处的切线方程为 ▲ .