题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)定义:对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的不动点.如果函数
的不动点.如果函数![]() 存在不动点,求实数
存在不动点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2) ![]()
【解析】
(1)对函数![]() 求导,结合二次函数的性质讨论
求导,结合二次函数的性质讨论![]() 的范围,即可判断
的范围,即可判断![]() 的单调性;(2)由
的单调性;(2)由![]() 存在不动点,得到
存在不动点,得到![]() 有实数根,即
有实数根,即![]() 有解,构造函数令
有解,构造函数令![]() ,通过求导即可判断
,通过求导即可判断![]() 的单调性,从而得到
的单调性,从而得到![]() 的取值范围,即可得到
的取值范围,即可得到![]() 的范围。
的范围。
(1)![]() 的定义域为
的定义域为![]() ,
,
对于函数![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 恒成立.
恒成立.
![]() 在
在![]() 恒成立.
恒成立.
![]() 在
在![]() 为增函数;
为增函数;
②当![]() ,即
,即![]() 或
或![]() 时,
时,
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ,
,![]() ,
,
![]() 在
在![]() 为增函数,
为增函数,![]() 减函数.
减函数.
![]() 为增函数,
为增函数,
当![]() 时,由
时,由![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 为增函数。
为增函数。
综上,当![]() 时,
时,![]() 在
在![]() 为增函数,
为增函数,![]() 减函数,
减函数,![]() 为增函数;当
为增函数;当![]() 时,
时,![]() 在
在![]() 为增函数。
为增函数。
(2)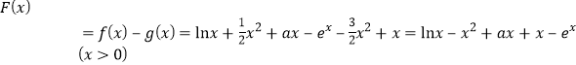 ,
,
![]() 存在不动点,
存在不动点,![]() 方程
方程![]() 有实数根,即
有实数根,即![]() 有解,
有解,
令![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增;
单调递增;
![]() ,
,
当![]() 时,
时,![]() 有不动点,
有不动点,
![]() 的范围为
的范围为![]() .
.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: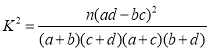 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期低于平均数的患者,称为“短潜伏者”,潜伏期不低于平均数的患者,称为“长潜伏者”.
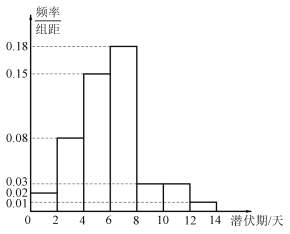
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |