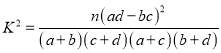题目内容
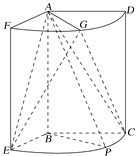
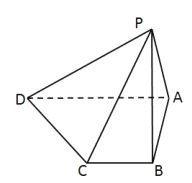
【题目】如图,已知多面体![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
(Ⅰ)由余弦定理得PB![]() ,从而PB⊥AB,由AD⊥平面PAB,得AD⊥PB,再由PB⊥AB,能证明PB⊥平面ABCD.
,从而PB⊥AB,由AD⊥平面PAB,得AD⊥PB,再由PB⊥AB,能证明PB⊥平面ABCD.
(Ⅱ)由余弦定理求出cos∠PDC![]() ,从而sin∠PCD
,从而sin∠PCD![]() ,S△ACD=2,设直线PA与平面PCD所成角为θ,点A到平面PCD的距离为h,由VA﹣PDC=VP﹣ACD,得h
,S△ACD=2,设直线PA与平面PCD所成角为θ,点A到平面PCD的距离为h,由VA﹣PDC=VP﹣ACD,得h![]() ,从而sinθ
,从而sinθ![]() ,由此能求出直线PA与平面PCD所成角的正弦值.
,由此能求出直线PA与平面PCD所成角的正弦值.
(Ⅰ)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() 四点共面.
四点共面.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)(方法一)在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() .
.
在直角梯形![]() 中,
中,![]() .
.
在![]() 中,
中,
![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,
,
故直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
(方法二)由(Ⅰ)知,![]() 平面
平面![]() ,
,![]() .
.
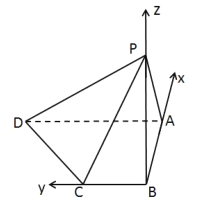
以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图的空间直角坐标系,
轴建立如图的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由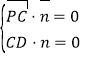 得
得![]() 取
取![]() ,
,
则![]() ,
,![]() ,所以
,所以![]() .
.
所以![]()
![]() ,
,
故直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
(方法三)延长![]() ,
,![]() 相交于点
相交于点![]() ,连结
,连结![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 为
为![]() 的中位线,
的中位线,
点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.所以
的中点.所以![]() 为等腰三角形.
为等腰三角形.
取![]() 中点
中点![]() ,连
,连![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
作![]() 于
于![]() ,连
,连![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以![]() ,
,
故直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

 应用题作业本系列答案
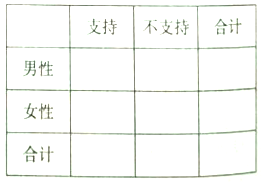
应用题作业本系列答案【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”