题目内容
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
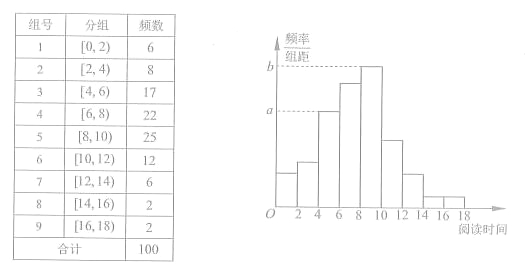
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)第4组.
;(3)第4组.
【解析】
试题(1)由频率分布表知,100人中有10人阅读时间不少于12小时,所以由对立事件的概率计算公式得p=![]() ;(2)由频率分表知,阅读时间在[4,6)的共17人,所以样本落在该组的概率为0.17,则频率分布直方图中样本落在[4,6)的小矩形的面积为0.17,从而求出矩形的高即a的值,同理得到b的值;(3)可以通过频率分布表或频率分布直方图求出平均数即可知平均数在那一组.
;(2)由频率分表知,阅读时间在[4,6)的共17人,所以样本落在该组的概率为0.17,则频率分布直方图中样本落在[4,6)的小矩形的面积为0.17,从而求出矩形的高即a的值,同理得到b的值;(3)可以通过频率分布表或频率分布直方图求出平均数即可知平均数在那一组.
试题解析:(1)根据频数分布表,100名学生中课外阅读时间不少于12小时的学生共有6+2+2=10名,所以样本中的学生课外阅读时间少于12小时的频率是![]() ;
;
(2)课外阅读时间落在[4,6)的有17人,频率为0.17,所以![]() ,
,
课外阅读时间落在[8,10)的有25人,频率为0.25,所以![]() ,
,
(3)估计样本中的100名学生课外阅读时间的平均数在第4组.

【题目】十九大指出,必须树立“绿水青山就是金山银山”的生态文明发展理念,这一理念将进一步推动新能源汽车产业的迅速发展![]() 以下是近几年我国新能源汽车的年销量数据及其散点图
以下是近几年我国新能源汽车的年销量数据及其散点图![]() 如图所示
如图所示![]() :
:
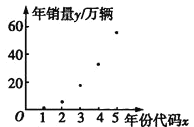
年份 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
新能源汽车的年销量 |
|
|
|
|
|
(1)请根据散点图判断![]() 与
与![]() 中哪个更适宜作为新能源汽车年销量
中哪个更适宜作为新能源汽车年销量![]() 关于年份代码
关于年份代码![]() 的回归方程模型?
的回归方程模型?![]() 给出判断即可,不必说明理由)
给出判断即可,不必说明理由)
(2)根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程,并预测2019年我国新能源汽车的年销量
的回归方程,并预测2019年我国新能源汽车的年销量![]() 精确到
精确到![]()
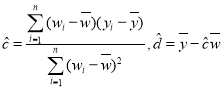
附令![]() ,
,
|
|
|
|
|
| 10 | 374 |
| 851.2 |