题目内容
已知函数f(x)=ax2+1,g(x)=x3+bx,其中a>0,b>0.
(1)若曲线y=f(x)与曲线y=g(x) 在它们的交点P(2,c)处有相同的切线(P为切点),求实数a,b的值;
(2)令h (x)=f(x)+g(x),若函数h(x)的单调减区间为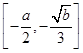 .
.
①求函数h(x)在区间(-∞,-1]上的最大值M(a);
②若|h(x)|≤3在x∈[-2,0]上恒成立,求实数a的取值范围.
(1)若曲线y=f(x)与曲线y=g(x) 在它们的交点P(2,c)处有相同的切线(P为切点),求实数a,b的值;
(2)令h (x)=f(x)+g(x),若函数h(x)的单调减区间为
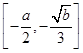 .
.①求函数h(x)在区间(-∞,-1]上的最大值M(a);
②若|h(x)|≤3在x∈[-2,0]上恒成立,求实数a的取值范围.
(1)a=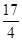 ,b=5
,b=5
(2)①M(a)=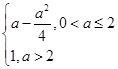
②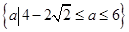
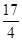 ,b=5
,b=5(2)①M(a)=
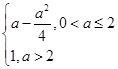
②
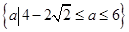
解:(1)由P(2,c)为公共切点,
f(x)=ax2+1,g(x)=x3+bx(a>0),
得f′(x)=2ax,k1=4a,
g′(x)=3x2+b,k2=12+b.
又f(2)=4a+1,g(2)=8+2b,
所以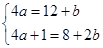 ,解得a=
,解得a=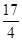 ,b=5.
,b=5.
(2)①h(x)=f(x)+g(x)
=x3+ax2+bx+1,
则h′(x)=3x2+2ax+b.
因为函数f(x)+g(x)的单调减区间为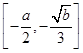 ,
,
所以x∈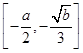 时,有3x2+2ax+b≤0恒成立.
时,有3x2+2ax+b≤0恒成立.
此时x=-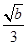 是方程3x2+2ax+b=0的一个根,
是方程3x2+2ax+b=0的一个根,
所以3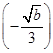 2+2a
2+2a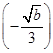 +b=0,
+b=0,
得a2=4b,
所以h(x)=f(x)+g(x)
=x3+ax2+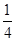 a2x+1.
a2x+1.
又函数h(x)在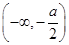 上单调递增,在
上单调递增,在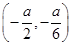 上单调递减,在
上单调递减,在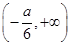 上单调递增.
上单调递增.
若-1≤-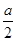 ,即a≤2时,
,即a≤2时,
最大值为h(-1)=a- ;
;
若-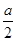 <-1<-
<-1<-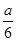 时,即2<a<6时,
时,即2<a<6时,
最大值为h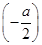 =1;
=1;
若-1≥-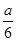 时,即a≥6时,
时,即a≥6时,
最大值为h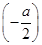 =1,
=1,
综上所述,M(a)=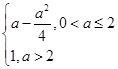
②由①可知h(x)在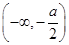 上单调递增,在
上单调递增,在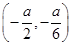 上单调递减,在
上单调递减,在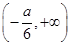 上单调递增.
上单调递增.
所以h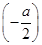 为极大值,h
为极大值,h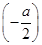 =1,
=1,
h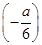 为极小值,h
为极小值,h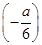 =-
=-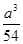 +1,
+1,
因为|h(x)|≤3在x∈[-2,0]上恒成立,
又h(0)=1,所以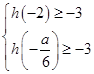
即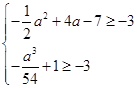
解得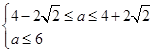
故实数a的取值范围是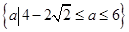 .
.
f(x)=ax2+1,g(x)=x3+bx(a>0),
得f′(x)=2ax,k1=4a,
g′(x)=3x2+b,k2=12+b.
又f(2)=4a+1,g(2)=8+2b,
所以
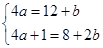 ,解得a=
,解得a=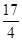 ,b=5.
,b=5.(2)①h(x)=f(x)+g(x)
=x3+ax2+bx+1,
则h′(x)=3x2+2ax+b.
因为函数f(x)+g(x)的单调减区间为
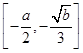 ,
,所以x∈
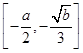 时,有3x2+2ax+b≤0恒成立.
时,有3x2+2ax+b≤0恒成立.此时x=-
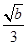 是方程3x2+2ax+b=0的一个根,
是方程3x2+2ax+b=0的一个根,所以3
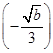 2+2a
2+2a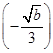 +b=0,
+b=0,得a2=4b,
所以h(x)=f(x)+g(x)
=x3+ax2+
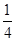 a2x+1.
a2x+1.又函数h(x)在
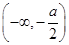 上单调递增,在
上单调递增,在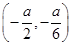 上单调递减,在
上单调递减,在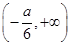 上单调递增.
上单调递增.若-1≤-
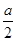 ,即a≤2时,
,即a≤2时,最大值为h(-1)=a-
 ;
;若-
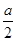 <-1<-
<-1<-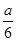 时,即2<a<6时,
时,即2<a<6时,最大值为h
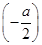 =1;
=1;若-1≥-
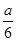 时,即a≥6时,
时,即a≥6时,最大值为h
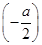 =1,
=1,综上所述,M(a)=
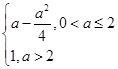
②由①可知h(x)在
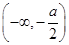 上单调递增,在
上单调递增,在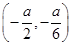 上单调递减,在
上单调递减,在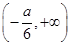 上单调递增.
上单调递增.所以h
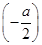 为极大值,h
为极大值,h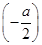 =1,
=1,h
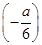 为极小值,h
为极小值,h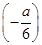 =-
=-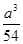 +1,
+1,因为|h(x)|≤3在x∈[-2,0]上恒成立,
又h(0)=1,所以
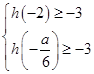
即
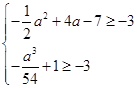
解得
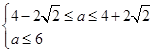
故实数a的取值范围是
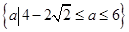 .
.
练习册系列答案
相关题目
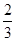 时,求函数y=f(x)的单调区间与极值.
时,求函数y=f(x)的单调区间与极值.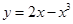 在横坐标为
在横坐标为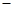 l的点处的切线为
l的点处的切线为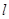 ,则点P(3,2)到直线
,则点P(3,2)到直线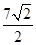
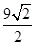
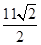
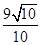
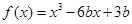 在(0,1)内有极小值,则实数b的取值范围是( )
在(0,1)内有极小值,则实数b的取值范围是( )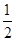 )
)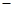 ∞,1)
∞,1)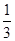 ,则f(x)<
,则f(x)< +
+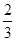 的解集为( )
的解集为( )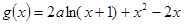 .
.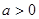 时,讨论函数
时,讨论函数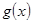 的单调性;
的单调性;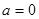 时,在函数
时,在函数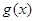 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为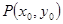 ,试探究函数
,试探究函数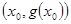 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?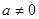 时
时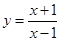 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则

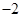

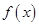 的导函数为
的导函数为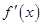 ,且满足关系式
,且满足关系式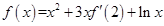 ,则
,则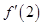 的值等于= .
的值等于= .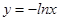 在点
在点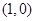 处的切线斜率为 .
处的切线斜率为 .