题目内容
已知两定点A、B,一动点P,如果∠PAB和∠PBA中的一个是另一个的2倍,求P点的轨迹方程.
P点轨迹方程为(x+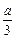 )2-
)2-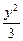 =
=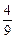 a2(y≠0).
a2(y≠0).
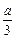 )2-
)2-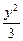 =
=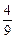 a2(y≠0).
a2(y≠0).认真分析题设条件,综合利用平面几何的知识,列出几何等式,再利用解析几何的一些概念、公式、定理等将几何等式坐标化,便得曲线的方程,还要将所得方程化简,使求得的方程是最简单的形式.
∵给出了∠PAB和∠PBA中的一个是另一个的2倍,即∠PAB=2∠PBA或∠PBA=" " 2∠PAB,将kPA、kPB代入二倍角公式,即得到P点的轨迹方程.
如下图所示建立直角坐标系.
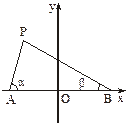
设A、B两点的坐标分别为(-a,0)、(a,0),P(x,y).
∵kPA=tanα=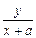 , ①
, ①
kPB=tan(180°-β)=-tanβ=-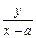 , ②
, ②
当α=2β时,tanα=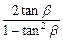 . ③
. ③
将①②代入③,得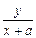 =
=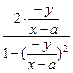 .
.
化简后得P点的轨迹方程为(x-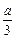 )2-
)2-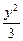 =
=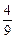 a2(y≠0).
a2(y≠0).
当点P在y轴右侧时,即β=2α,同时可得P点轨迹方程为(x+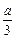 )2-
)2-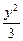 =
=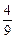 a2(y≠0).
a2(y≠0).
∵给出了∠PAB和∠PBA中的一个是另一个的2倍,即∠PAB=2∠PBA或∠PBA=" " 2∠PAB,将kPA、kPB代入二倍角公式,即得到P点的轨迹方程.
如下图所示建立直角坐标系.

设A、B两点的坐标分别为(-a,0)、(a,0),P(x,y).
∵kPA=tanα=
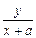 , ①
, ①kPB=tan(180°-β)=-tanβ=-
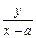 , ②
, ②当α=2β时,tanα=
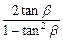 . ③
. ③将①②代入③,得
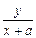 =
=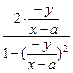 .
.化简后得P点的轨迹方程为(x-
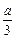 )2-
)2-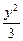 =
=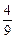 a2(y≠0).
a2(y≠0).当点P在y轴右侧时,即β=2α,同时可得P点轨迹方程为(x+
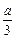 )2-
)2-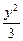 =
=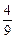 a2(y≠0).
a2(y≠0).
练习册系列答案
相关题目
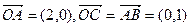 ,动点
,动点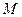 到定直线
到定直线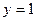 的距离等于
的距离等于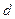 ,并且满足
,并且满足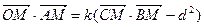 ,其中
,其中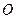 为坐标原点,
为坐标原点,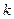 为非负实数.
为非负实数.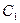 ;
;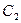 ,试判断曲线
,试判断曲线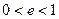 ,当
,当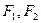 是曲线
是曲线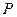 ,使得
,使得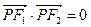 成立,求实数
成立,求实数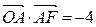 ,则点A的坐标为……( )
,则点A的坐标为……( )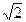 )
)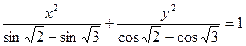 表示的曲线是( )
表示的曲线是( )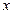 轴上的椭圆
轴上的椭圆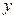 轴上的椭圆
轴上的椭圆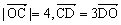 ,动点M到直线AB的距离是它到点D的距离的2倍。
,动点M到直线AB的距离是它到点D的距离的2倍。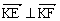 ,动点P满足
,动点P满足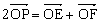 ,求直线KP的斜率的取值范围。
,求直线KP的斜率的取值范围。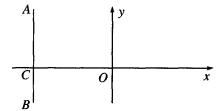
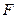 在
在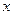 轴上,
轴上,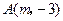 在抛物线上,且
在抛物线上,且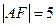 ,求抛物线的标准方程.
,求抛物线的标准方程.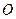 为抛物线
为抛物线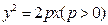 的顶点,
的顶点,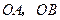 为这条抛物线互相垂直的两条动弦.
为这条抛物线互相垂直的两条动弦.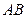 必过一定点.
必过一定点.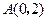 的距离减去它到
的距离减去它到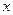 轴的距离的差是
轴的距离的差是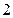 ,求这曲线的方程.
,求这曲线的方程.