Question

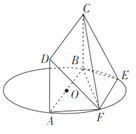
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N。

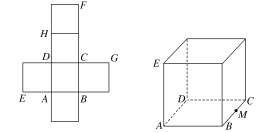
(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；

(2)证明：直线MN∥平面BDH；

(3)过点M，N，H的平面将正方体分割为两部分，求这两部分的体积比．

Answer 1

【答案】见解析

【解析】解：(1)点F，G，H的位置如图所示．

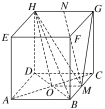
(2)证明：连接BD，设O为BD的中点，连接OM，OH，AC，BH，MN。

∵M，N分别是BC，GH的中点，

∴OM∥CD，且OM＝CD，NH∥CD，且NH＝CD，

∴OM∥NH，OM＝NH，

则四边形MNHO是平行四边形，∴MN∥OH，

又∵MN平面BDH，OH平面BDH，

∴MN∥平面BDH。

(3)由(2)知OM∥NH，OM＝NH，连接GM，MH，过点M，N，H的平面就是平面GMH，它将正方体分割为两个同高的棱柱，高都是GH，底面分别是四边形BMGF和三角形MGC，

体积比等于底面积之比，即3∶1。