题目内容
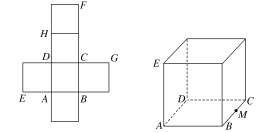
【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
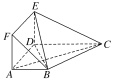
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
【答案】见解析
【解析】
解:(1)证明:因为AD=1,CD=2,AC=![]() ,
,
所以AD2+CD2=AC2,
所以△ADC为直角三角形,且AD⊥DC.
同理,因为ED=1,CD=2,EC=![]() ,
,
所以ED2+CD2=EC2,
所以△EDC为直角三角形,且ED⊥DC.
又四边形ADEF是正方形,所以AD⊥DE,
又AD∩DC=D,所以ED⊥平面ABCD.
又BC平面ABCD,所以ED⊥BC.
在梯形ABCD中,过点B作BH⊥CD于点H,
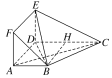
故四边形ABHD是正方形,所以∠ADB=45°,BD=![]() 。
。
在Rt△BCH中,BH=CH=1,所以BC=![]() ,
,
故BD2+BC2=DC2,所以BC⊥BD.
因为BD∩ED=D,BD平面EBD,ED平面EBD,
所以BC⊥平面EBD,
又BC平面EBC,所以平面EBC⊥平面EBD.
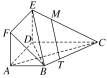
(2)在线段BC上存在一点T,使得MT∥平面BDE,此时3BT=BC.
连接MT,在△EBC中,因为![]() =
=![]() =
=![]() ,所以MT∥EB.
,所以MT∥EB.
又MT平面BDE,EB平面BDE,
所以MT∥平面BDE。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目