题目内容
9．函数y=|x-2|的单调递增区间为[2，+∞）．分析 画出函数y=|x-2|的图象，数形结合可得函数的增区间．
解答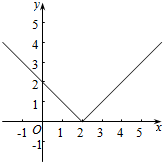 
解：函数y=|x-2|的图象如图所示：
数形结合可得函数的增区间为[2，+∞），
故答案为：[2，+∞）．
点评 本题主要考查函数的图象特征，函数的单调性的判断，体现了数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
17．在等比数列{an}中，a1=2，an+1=3an，则其前n项和为Sn的值为（ ）
| A． | 3n-1 | B． | 1-3n | C． | $\frac{1}{{{3^{n-1}}}}-1$ | D． | $1-\frac{1}{{{3^{n-1}}}}$ |
19．抽取某种型号的车床生产的10个零件，编号为A1，A2，…，A10，测量其直径（单位：cm），得到下面数据：
其中直径在区间[1.49，1.51]内的零件为一等品．
（1）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（2）从一等品零件中，随机抽取2个．
①用零件的编号列出所有可能的抽取结果；
②求这2个零件直径相等的概率；
（3）若甲、乙分别从一等品中各取一个，求甲取到零件的直径大于乙取到零件的直径的概率．
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.48 | 1.47 | 1.53 | 1.52 | 1.47 |
（1）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（2）从一等品零件中，随机抽取2个．
①用零件的编号列出所有可能的抽取结果；
②求这2个零件直径相等的概率；
（3）若甲、乙分别从一等品中各取一个，求甲取到零件的直径大于乙取到零件的直径的概率．