题目内容
【题目】某运输公司接受了向一地区每天至少运送180 t物资的任务，该公司有8辆载重为6 t的A型卡车和4辆载重为10 t的B型卡车，有10名驾驶员，每辆卡车每天往返的次数为A型卡车4次，B型卡车3次，每辆卡车每天往返的费用为A型卡车320元，B型卡车504元，则公司如何调配车辆，才能使公司所花的费用最低，最低费用为________元.
【答案】2560
【解析】设每天调出A型卡车x辆，B型卡车y辆，公司所花的费用为z元，则目标函数z＝320x＋504y(x，y∈N)．
由题意可得，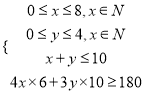 
作出上述不等式组所确定的平面区域即可行域，如图中阴影部分所示．
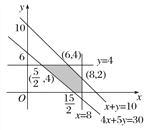
结合图形可知，z＝320x＋504y在可行域内经过的整数点中，点(8,0)使z＝320x＋504y取得最小值，zmin＝320×8＋504×0＝2 560.
故每天调出A型卡车8辆，公司所花费用最低为2 560元．
练习册系列答案
相关题目
