题目内容
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数, ![]() ).
).
(1)讨论函数![]() 的单调性;
的单调性;
(2)当函数![]() 有两个零点
有两个零点![]() 时,证明:
时,证明: ![]() .
.
【答案】(1) 当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在R上单调递增.(2)见解析.
在R上单调递增.(2)见解析.
【解析】试题分析:(1)对![]() 求导,再对
求导,再对![]() 进行分类讨论,根据导数与函数的单调性的关系,即可求得函数
进行分类讨论,根据导数与函数的单调性的关系,即可求得函数![]() 的单调性;(2)当
的单调性;(2)当![]() 时,由(1)知函数
时,由(1)知函数![]() 单调递增,不存在两个零点,故
单调递增,不存在两个零点,故![]() ,设函数
,设函数![]() 的两个零点为
的两个零点为![]() ,代入到
,代入到![]() ,可得
,可得![]() ,作差后,令
,作差后,令![]() 结合
结合![]() ,求得
,求得![]() ,欲证
,欲证![]() ,只需证明
,只需证明![]() ,构造
,构造![]() ,求导,根据函数的单调性即可求得
,求导,根据函数的单调性即可求得![]() ,从而证出
,从而证出![]() .
.
试题解析:(1)解:∵![]()
∴当![]() 时,令
时,令![]() ,即当
,即当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,即函数
,即函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 恒成立,故此时函数
恒成立,故此时函数![]() 在R上单调递增.
在R上单调递增.
(2)证明:当![]() 时,由(1)知函数
时,由(1)知函数![]() 单调递增,不存在两个零点,所以
单调递增,不存在两个零点,所以![]()
设函数![]() 的两个零点为
的两个零点为![]() ,则
,则![]()
∴![]()
∴![]()
设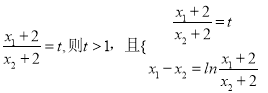
解得![]() ,所以
,所以![]()
欲证![]() ,只需证明
,只需证明![]()
设![]() ,则
,则![]()
设![]() ,则
,则![]() 单调递增
单调递增
∴![]()
∴![]() 在区间
在区间![]() 上单调递增
上单调递增
∴![]()
∴![]() ,故
,故![]() 成立.
成立.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
【题目】某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
组别 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0.16 |
第2组 | [60,70) | a | ■ |
第3组 | [70,80) | 20 | 0.40 |
第4组 | [80,90) | ■ | 0.08 |
第5组 | [90,100] | 2 | b |
合计 | ■ | ■ |
(1)求出a,b的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.
①求所抽取的2名同学中至少有1名同学来自第5组的概率;
②求所抽取的2名同学来自同一组的概率.