题目内容
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

【答案】(1)最大值为400.(2)当![]() 时,
时, ![]() 最大
最大![]() 平方米,此时
平方米,此时![]() .
.
【解析】试题分析:(1)步道长为扇形周长![]() ,利用弧长公式及扇形面积公式可得不等式
,利用弧长公式及扇形面积公式可得不等式![]() ,利用基本不等式将不等式转化为关于
,利用基本不等式将不等式转化为关于![]() 的一元不等式,解得
的一元不等式,解得![]() 的范围,确定最大值为400.(2)由条件得
的范围,确定最大值为400.(2)由条件得![]() ,消
,消![]() 得
得![]() ,由
,由![]() 及
及![]() ,解出
,解出![]() ,根据二次函数最值取法得到当
,根据二次函数最值取法得到当![]() 时,
时, ![]() 最大
最大![]()
试题解析:解:(1)由题意,弧长![]() 为
为![]() ,扇形面积为
,扇形面积为![]() ,
,
由题意![]() ,即
,即![]() ,
,
即![]() ,
,
所以![]() ,所以
,所以![]() ,
, ![]() ,则
,则![]() ,
,
所以当![]() 时,面积
时,面积![]() 的最大值为400.
的最大值为400.
(2)即![]() ,
, ![]() 代入可得
代入可得
![]() 或
或![]() ,
,
又![]() ,
,
当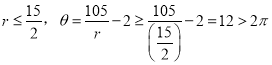 与
与![]() 不符,
不符,
![]() 在
在![]() 上单调,当
上单调,当![]() 时,
时, ![]() 最大
最大![]() 平方米,此时
平方米,此时![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目