题目内容
(理)命题“若两个正实数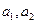 满足
满足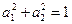 ,那么
,那么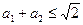 。”
。”
证明如下:构造函数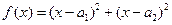 ,因为对一切实数
,因为对一切实数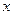 ,恒有
,恒有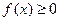 ,
,
又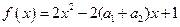 ,从而得
,从而得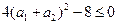 ,所以
,所以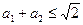 。
。
根据上述证明方法,若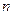 个正实数满足
个正实数满足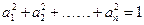 时,你可以构造函数
时,你可以构造函数
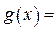 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).
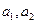 满足
满足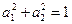 ,那么
,那么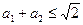 。”
。”证明如下:构造函数
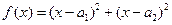 ,因为对一切实数
,因为对一切实数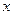 ,恒有
,恒有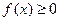 ,
,又
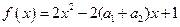 ,从而得
,从而得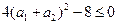 ,所以
,所以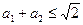 。
。根据上述证明方法,若
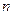 个正实数满足
个正实数满足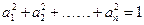 时,你可以构造函数
时,你可以构造函数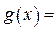 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).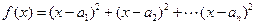 ,
, 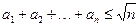
略

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 (本题12分)已知函数
(本题12分)已知函数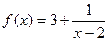 ,
,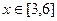 .
. 的单调性,并用定义加以证明;
的单调性,并用定义加以证明; (2)求函数
(2)求函数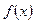 在
在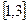 上为增函数,且有最小值0,则它在
上为增函数,且有最小值0,则它在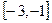 上( )
上( )
 总有
总有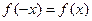 ,且
,且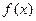 在区间
在区间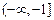 上是增函数,则 ( )
上是增函数,则 ( )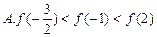
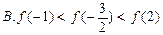
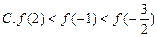
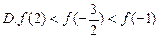
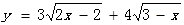 最大值为 ( )
最大值为 ( )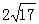
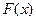 和
和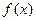 都在区间
都在区间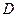 上有定义,若对
上有定义,若对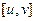 ,总有
,总有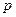 和
和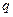 ,使得不等式
,使得不等式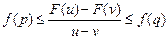 成立,则称
成立,则称 在区间
在区间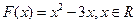 ,那么
,那么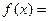 _____________
_____________ 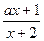 在区间(-2,+
在区间(-2,+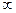 )上是增函数,则a的取值范围是 .
)上是增函数,则a的取值范围是 . 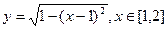 对于满足
对于满足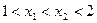 的任意
的任意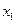 ,
,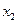 ,给出下列结论:
,给出下列结论: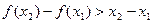 ; ②
; ②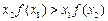 ;
;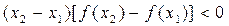 . ④
. ④