题目内容
设函数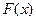 和
和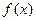 都在区间
都在区间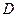 上有定义,若对
上有定义,若对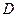 的任意子区间
的任意子区间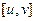 ,总有
,总有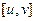 上的实数
上的实数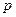 和
和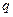 ,使得不等式
,使得不等式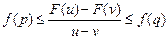 成立,则称
成立,则称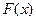 是
是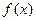 在区间
在区间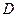 上的甲函数,
上的甲函数,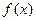 是
是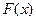
 在区间
在区间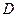 上的乙函数.已知
上的乙函数.已知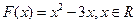 ,那么
,那么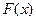 的乙函数
的乙函数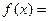 _____________
_____________
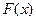 和
和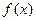 都在区间
都在区间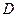 上有定义,若对
上有定义,若对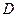 的任意子区间
的任意子区间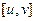 ,总有
,总有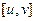 上的实数
上的实数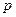 和
和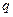 ,使得不等式
,使得不等式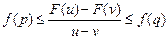 成立,则称
成立,则称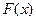 是
是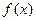 在区间
在区间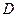 上的甲函数,
上的甲函数,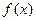 是
是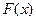
 在区间
在区间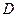 上的乙函数.已知
上的乙函数.已知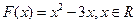 ,那么
,那么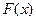 的乙函数
的乙函数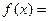 _____________
_____________ 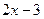
略

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
题目内容
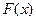 和
和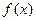 都在区间
都在区间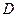 上有定义,若对
上有定义,若对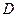 的任意子区间
的任意子区间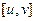 ,总有
,总有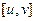 上的实数
上的实数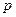 和
和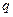 ,使得不等式
,使得不等式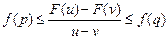 成立,则称
成立,则称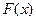 是
是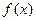 在区间
在区间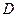 上的甲函数,
上的甲函数,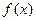 是
是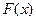
 在区间
在区间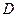 上的乙函数.已知
上的乙函数.已知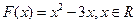 ,那么
,那么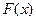 的乙函数
的乙函数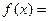 _____________
_____________ 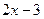

 初中暑期衔接系列答案
初中暑期衔接系列答案