题目内容
已知函数 (
( 、
、 ∈R,
∈R, ≠0),函数
≠0),函数 的图象在点(2,
的图象在点(2, )处的切线与
)处的切线与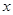 轴平行.
轴平行.
(1)用关于 的代数式表示
的代数式表示 ;
;
(2)求函数 的单调增区间;
的单调增区间;
(3)当 ,若函数
,若函数 有三个零点,求m的取值范围.
有三个零点,求m的取值范围.
 (
( 、
、 ∈R,
∈R, ≠0),函数
≠0),函数 的图象在点(2,
的图象在点(2, )处的切线与
)处的切线与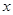 轴平行.
轴平行.(1)用关于
 的代数式表示
的代数式表示 ;
;(2)求函数
 的单调增区间;
的单调增区间;(3)当
 ,若函数
,若函数 有三个零点,求m的取值范围.
有三个零点,求m的取值范围.(1) (2)当
(2)当 时,函数
时,函数 的单调增区间是(-∞,0)和(2,+∞);当
的单调增区间是(-∞,0)和(2,+∞);当 时,函数
时,函数 的单调增区间是(0,2) (3)
的单调增区间是(0,2) (3) .
.
 (2)当
(2)当 时,函数
时,函数 的单调增区间是(-∞,0)和(2,+∞);当
的单调增区间是(-∞,0)和(2,+∞);当 时,函数
时,函数 的单调增区间是(0,2) (3)
的单调增区间是(0,2) (3) .
.(1)由于 可找到m、n的等式关系.从而可以用m表示n.
可找到m、n的等式关系.从而可以用m表示n.
(2) 利用导数大于(小于)零,求出函数的单调增(减)区间.
(3) 当m>0时,函数 有三个零点,可转化为方程f(x)=m-1有三个不同的实数根,
有三个零点,可转化为方程f(x)=m-1有三个不同的实数根,
进一步转化为函数y=f(x)与直线y=m-1有三个不同的交点,从而利用导数研究f(x)的图像的单调性极值来解决即可
(1)由已知条件得 ,又
,又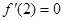 , ∴
, ∴ ,故
,故 .
.
(2)∵ ,∴
,∴ ,∴
,∴ . 令
. 令 ,即
,即 ,
,
当 时,解得
时,解得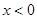 或
或 ,则函数
,则函数 的单调增区间是(-∞,0)和(2,+∞);
的单调增区间是(-∞,0)和(2,+∞);
当 时,解得
时,解得 ,则函数
,则函数 的单调增区间是(0,2).………………8分
的单调增区间是(0,2).………………8分
综上,当 时,函数
时,函数 的单调增区间是(-∞,0)和(2,+∞);当
的单调增区间是(-∞,0)和(2,+∞);当 时,
时,
函数 的单调增区间是(0,2).………………………10分
的单调增区间是(0,2).………………………10分
(3)由 及
及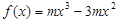
当 ,
, ,
,

当 ,解得
,解得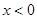 或
或 ,则函数
,则函数 的单调增区间是(-∞,0)和(2,+∞);
的单调增区间是(-∞,0)和(2,+∞);
当 ,得
,得 ,则函数
,则函数 的单调减区间是(0,2),……………12分
的单调减区间是(0,2),……………12分
所以 有极大值
有极大值 和极小值
和极小值 ,
,
因为 有三个零点,则
有三个零点,则 得
得 .
.
 可找到m、n的等式关系.从而可以用m表示n.
可找到m、n的等式关系.从而可以用m表示n.(2) 利用导数大于(小于)零,求出函数的单调增(减)区间.
(3) 当m>0时,函数
 有三个零点,可转化为方程f(x)=m-1有三个不同的实数根,
有三个零点,可转化为方程f(x)=m-1有三个不同的实数根,进一步转化为函数y=f(x)与直线y=m-1有三个不同的交点,从而利用导数研究f(x)的图像的单调性极值来解决即可
(1)由已知条件得
 ,又
,又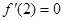 , ∴
, ∴ ,故
,故 .
.(2)∵
 ,∴
,∴ ,∴
,∴ . 令
. 令 ,即
,即 ,
,当
 时,解得
时,解得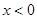 或
或 ,则函数
,则函数 的单调增区间是(-∞,0)和(2,+∞);
的单调增区间是(-∞,0)和(2,+∞);当
 时,解得
时,解得 ,则函数
,则函数 的单调增区间是(0,2).………………8分
的单调增区间是(0,2).………………8分综上,当
 时,函数
时,函数 的单调增区间是(-∞,0)和(2,+∞);当
的单调增区间是(-∞,0)和(2,+∞);当 时,
时,函数
 的单调增区间是(0,2).………………………10分
的单调增区间是(0,2).………………………10分(3)由
 及
及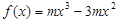
当
 ,
, ,
,
当
 ,解得
,解得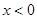 或
或 ,则函数
,则函数 的单调增区间是(-∞,0)和(2,+∞);
的单调增区间是(-∞,0)和(2,+∞);当
 ,得
,得 ,则函数
,则函数 的单调减区间是(0,2),……………12分
的单调减区间是(0,2),……………12分所以
 有极大值
有极大值 和极小值
和极小值 ,
,因为
 有三个零点,则
有三个零点,则 得
得 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
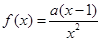 ,其中
,其中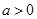 。
。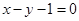 是曲线
是曲线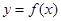 的切线,求a的值;
的切线,求a的值;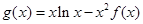 ,求
,求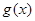 在区间
在区间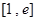 上的最大值。(其中e为自然对数的底数)。
上的最大值。(其中e为自然对数的底数)。 天
天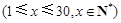 的销售价格为
的销售价格为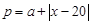 (
(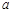 为常数)(元∕件),第
为常数)(元∕件),第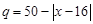 (件),且公司在第
(件),且公司在第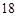 天该产品的销售收入为
天该产品的销售收入为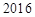 元.
元.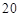 天该产品的销售收入是多少?
天该产品的销售收入是多少?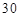 天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
天中该公司在哪一天该产品的销售收入最大?最大收入为多少?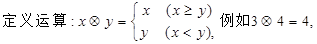 则下列等式不能成立的是( )
则下列等式不能成立的是( )


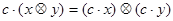 (其中
(其中 )
) ,其中
,其中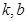 是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数
是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数 ,在已知点
,在已知点 附近一点
附近一点 的函数值
的函数值 ,利用这一方法,对于实数
,利用这一方法,对于实数 ,取
,取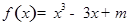 ,在
,在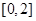 上任取三个数
上任取三个数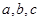 ,以
,以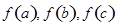 为边均可构成的三角形,则
为边均可构成的三角形,则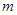 的范围是( )
的范围是( )

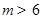

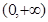 上为增函数的是( )
上为增函数的是( ) ;
; ;
; ;
; ;
;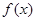 ,有下述命题:
,有下述命题: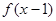 的图象关于点A(1,0)对称
的图象关于点A(1,0)对称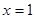 对称,则
对称,则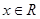 ,有
,有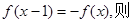 2是
2是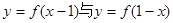 的图象关于直线
的图象关于直线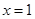 对称.
对称.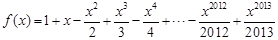 ,
,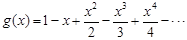
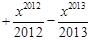 ,若函数
,若函数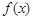 有唯一零点
有唯一零点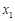 ,函数
,函数 有唯一零点
有唯一零点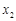 ,则有( )
,则有( )