题目内容
3.设函数f(x)=$\frac{1}{3}$mx3+(m+4)x2,g(x)=alnx,其中a≠0,当a=8时,设F(x)=f′(x)+g(x),讨论F(x)的单调性.分析 利用导函数的正负性判断原函数的单调性,注意要以m进行讨论.
解答 解:f′(x)=mx2+2(4+m)x,当a=8时,F(x)=mx2+2(4+m)x+8lnx,定义域为(0,+∞),
F'(x)=2mx+8+2m+$\frac{8}{x}$=$\frac{2m{x}^{2}+(8+2m)x+8}{x}$,
∵x>0,∴x+1>0,
①当m≥0时,F′(x)>0,此时F(x)在(0,+∞)上单调递增;
②当m<0时,由F′(x)>0,得0<x<$\frac{4}{m}$,由F′(x)<0得x>-$\frac{4}{m}$,
此时F(x)在(0,-$\frac{4}{m}$)上单调递增,在(-$\frac{4}{m},+∞$)上单调递减.
综上得:
当m≥0时,F(x)在(0,+∞)是上单调递增;
当m<0时,F(x)在(0,-$\frac{4}{m}$)上单调递增,在(-$\frac{4}{m},+∞$)上单调递减.
点评 本题考查了导数在函数中的应用,分类讨论思想,化归思想.属于常考题型,注意参数的讨论.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
14.执行右面的程序框图,若输入x=7,y=6,则输出的有数对为( )
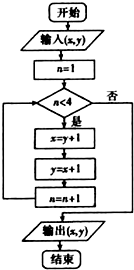

| A. | (11,12) | B. | (12,13) | C. | (13,14) | D. | (13,12) |
8.双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,直线l过焦点F,且斜率为k,则直线l与双曲线C的左、右两支都相交的充要条件是( )
| A. | k>-$\frac{b}{a}$ | B. | k<$\frac{b}{a}$ | C. | k>$\frac{b}{a}$或k<-$\frac{b}{a}$ | D. | -$\frac{b}{a}$<k<$\frac{b}{a}$ |
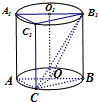 如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P
如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P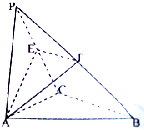 如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.