题目内容
【题目】设a为实数,函数![]() ,
,![]()
![]() 若
若![]() ,求不等式
,求不等式![]() 的解集;
的解集;
![]() 是否存在实数a,使得函数
是否存在实数a,使得函数![]() 在区间
在区间![]() 上既有最大值又有最小值?若存在,求出实数a的取值范围;若不存在,请说明理由;
上既有最大值又有最小值?若存在,求出实数a的取值范围;若不存在,请说明理由;
![]() 写出函数
写出函数![]() 在R上的零点个数
在R上的零点个数![]() 不必写出过程
不必写出过程![]()
【答案】(1)![]() ;(2)不存在;(3)3.
;(2)不存在;(3)3.
【解析】
![]() 代入a的值,通过讨论a的范围,求出不等式的解集即可;
代入a的值,通过讨论a的范围,求出不等式的解集即可;
![]() 通过讨论a的范围,求出函数的单调区间,求出函数的最值,得到关于a的不等式组,解出判断即可;
通过讨论a的范围,求出函数的单调区间,求出函数的最值,得到关于a的不等式组,解出判断即可;
![]() 通过讨论a的范围,判断函数的零点个数即可.
通过讨论a的范围,判断函数的零点个数即可.
(1)由题意,当![]() 时,
时,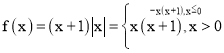 ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
故不存在这样的实数x,
当![]() 时,
时,![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
故不等式![]() 的解集是
的解集是![]() ;
;
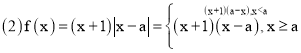 ,
,
![]() 若
若![]() ,则
,则![]() 在
在![]() 递增,在
递增,在![]() 递减,在
递减,在![]() 递增,
递增,
![]() 函数
函数![]() 在
在![]() 上既有最大值又有最小值,
上既有最大值又有最小值,
![]() ,
,![]() ,
,
从而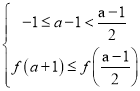 ,即
,即![]() ,
,
解得: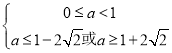 ,
,
故不存在这样的实数a;
![]() 若
若![]() ,则
,则![]() 在
在![]() 递增,在
递增,在![]() 递减,在
递减,在![]() 递增,
递增,
![]() 函数
函数![]() 在区间
在区间![]() 上既有最大值又有最小值,
上既有最大值又有最小值,
故![]() ,
,![]() ,
,
从而 ,即
,即![]() ,
,
解得: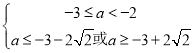 ,
,
故不存在这样的实数a;
![]() 若
若![]() ,则
,则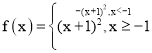 为R上的递增函数,
为R上的递增函数,
故![]() 在
在![]() 上不存在最大值又有最小值,
上不存在最大值又有最小值,
综上,不存在这样的实数a;
![]() 当
当![]() 或
或![]() 时,函数
时,函数![]() 的零点个数为1,
的零点个数为1,
当![]() 或
或![]() 时,函数
时,函数![]() 的零点个数为2,
的零点个数为2,
当![]() 时,函数
时,函数![]() 的零点个数为3.
的零点个数为3.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目

