题目内容
.选修4-1:几何证明选讲:
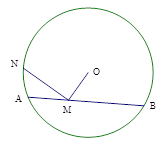
如图,在Rt△ABC中,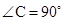 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,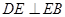 .
.

(Ⅰ)求证:AC是△BDE的外接圆的切线;
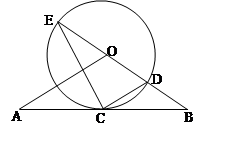
(Ⅱ)若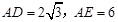 ,求EC的长.
,求EC的长.
如图,在Rt△ABC中,
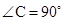 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,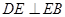 .
.
(Ⅰ)求证:AC是△BDE的外接圆的切线;
(Ⅱ)若
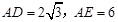 ,求EC的长.
,求EC的长.(Ⅰ)见解析;(Ⅱ) EC=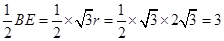 .
.
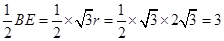 .
. (I)只需证明:设圆心为O,则证明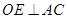 即可.进一步可考虑证明OE//BC.
即可.进一步可考虑证明OE//BC.
(II)可以利用切割线定理解决,先通过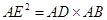 ,求出半径长,再利用OE//BC,可得
,求出半径长,再利用OE//BC,可得 ,求出EC的长.
,求出EC的长.
(Ⅰ)取BD的中点O,连接OE.
∵BE平分∠ABC,∴∠CBE=∠OBE.又∵OB=OE,∴∠OBE=∠BEO,
∴∠CBE=∠BEO,∴BC∥OE.………………3分
∵∠C=90°,∴OE⊥AC,∴AC是△BDE的外接圆的切线. --------------------5分
(Ⅱ)设⊙O的半径为r,则在△AOE中,
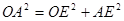 ,即
,即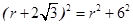 ,解得
,解得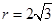 ,
,
∴OA=2OE, ∴∠A=30°,∠AOE=60°. ∴∠CBE=∠OBE=30°.
∴EC=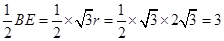 . ------------------------------10分
. ------------------------------10分
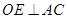 即可.进一步可考虑证明OE//BC.
即可.进一步可考虑证明OE//BC.(II)可以利用切割线定理解决,先通过
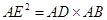 ,求出半径长,再利用OE//BC,可得
,求出半径长,再利用OE//BC,可得 ,求出EC的长.
,求出EC的长.(Ⅰ)取BD的中点O,连接OE.
∵BE平分∠ABC,∴∠CBE=∠OBE.又∵OB=OE,∴∠OBE=∠BEO,
∴∠CBE=∠BEO,∴BC∥OE.………………3分
∵∠C=90°,∴OE⊥AC,∴AC是△BDE的外接圆的切线. --------------------5分
(Ⅱ)设⊙O的半径为r,则在△AOE中,
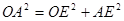 ,即
,即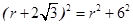 ,解得
,解得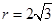 ,
, ∴OA=2OE, ∴∠A=30°,∠AOE=60°. ∴∠CBE=∠OBE=30°.
∴EC=
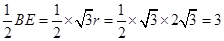 . ------------------------------10分
. ------------------------------10分
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
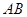 经过⊙
经过⊙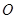 上的点
上的点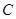 ,并且
,并且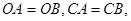 ⊙
⊙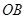 于
于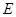 ,
,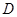 ,连接
,连接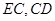 .
.
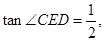 ⊙
⊙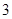 ,求
,求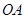 的长.
的长.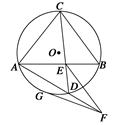
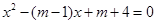 的两根,
的两根,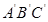 与△ABC开始时完全重合,然后让△ABC固定不动,将
与△ABC开始时完全重合,然后让△ABC固定不动,将 平方厘米?
平方厘米?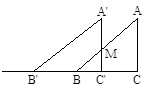
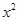 -7
-7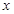 +12=0的两根,则
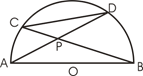
+12=0的两根,则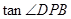 =_________。
=_________。
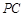 切⊙
切⊙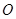 于点
于点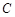 ,割线
,割线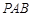 经过圆心
经过圆心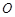 ,弦
,弦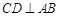 于点
于点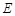 .已知⊙
.已知⊙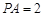 ,则
,则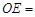 .
.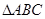 的
的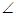
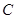 的平分线
的平分线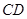 延长后交圆于点
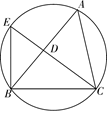
延长后交圆于点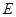 , 连接
, 连接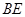 , 已知
, 已知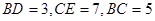 , 则线段
, 则线段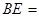 ( )
( ) 
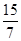
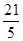
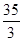
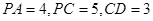 ,则
,则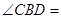 ( )
( )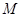 为
为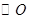 的弦
的弦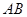 上的一点,连接
上的一点,连接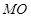 .
.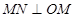 ,
,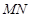 交圆于
交圆于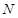 ,若
,若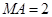 ,
,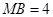 ,则
,则 .
.