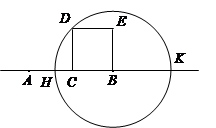题目内容
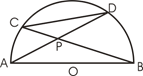
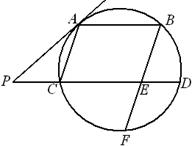
如图:AB是半圆O的直径,弦AD、BC相交于点P,且CD、AB的长分别是一元二次方程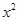 -7
-7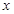 +12=0的两根,则
+12=0的两根,则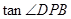 =_________。
=_________。
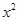 -7
-7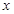 +12=0的两根,则
+12=0的两根,则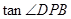 =_________。
=_________。
解:连接BD,则∠ADB=90°.
解方程x2-7x+12=0,可得x=3,x=4.
由于AB>CD,所以AB=4,CD=3.
由圆周角定理知:∠C=∠A,∠CDA=∠ABP.
故△CPD∽△APB,得PD: BP ="CD" :AB ="3" :4 .
设PD=3x,则BP=4x.
在Rt△PBD中,由勾股定理得:BD2= PB2-PD2 =" 7" x.
故tan∠DPB="BD" :PD =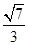
解方程x2-7x+12=0,可得x=3,x=4.
由于AB>CD,所以AB=4,CD=3.
由圆周角定理知:∠C=∠A,∠CDA=∠ABP.
故△CPD∽△APB,得PD: BP ="CD" :AB ="3" :4 .
设PD=3x,则BP=4x.
在Rt△PBD中,由勾股定理得:BD2= PB2-PD2 =" 7" x.
故tan∠DPB="BD" :PD =

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
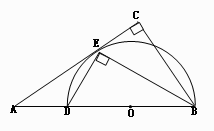
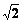 ,求BC的长。
,求BC的长。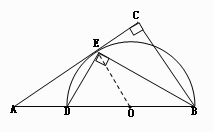
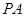 与圆
与圆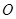 相切于点
相切于点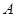 ,经过点
,经过点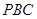 交圆
交圆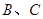 ,
,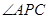 的平分线分别交
的平分线分别交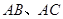 于点
于点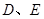 .
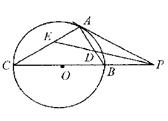
.
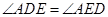 ;
;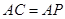 ,求
,求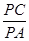 的值.
的值.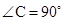 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,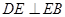 .
.
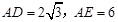 ,求EC的长.
,求EC的长.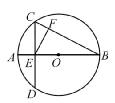
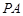 与⊙
与⊙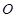 相切于点
相切于点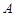 ,
,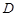 为
为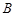 ,
,
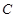 两点,若
两点,若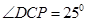 ,则
,则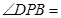 .
.