��Ŀ����
��֪����ͼ����Rt��ABC�У�б��AB��5���ף�BC��a���ף�AC��b���ף�a��b����a��b�Ƿ���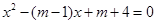 ��������
��������
����a��b��ֵ��
�ơ�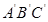 ���ABC��ʼʱ��ȫ�غϣ�Ȼ���á�ABC�̶���������
���ABC��ʼʱ��ȫ�غϣ�Ȼ���á�ABC�̶���������
��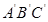 ��1����/����ٶ���BC���ڵ�ֱ�������ƶ�.
��1����/����ٶ���BC���ڵ�ֱ�������ƶ�.
��)��x����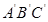 ���ABC ���ص����ֵ����Ϊyƽ�����ף���y��x֮��ĺ�����ϵʽ,��д��x��ȡֵ��Χ��
���ABC ���ص����ֵ����Ϊyƽ�����ף���y��x֮��ĺ�����ϵʽ,��д��x��ȡֵ��Χ��
��)������ص����ֵ��������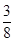 ƽ�����ף�
ƽ�����ף�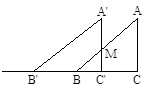
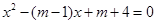 ��������
������������a��b��ֵ��
�ơ�
 ���ABC��ʼʱ��ȫ�غϣ�Ȼ���á�ABC�̶���������
���ABC��ʼʱ��ȫ�غϣ�Ȼ���á�ABC�̶�����������
 ��1����/����ٶ���BC���ڵ�ֱ�������ƶ�.
��1����/����ٶ���BC���ڵ�ֱ�������ƶ�.��)��x����
 ���ABC ���ص����ֵ����Ϊyƽ�����ף���y��x֮��ĺ�����ϵʽ,��д��x��ȡֵ��Χ��
���ABC ���ص����ֵ����Ϊyƽ�����ף���y��x֮��ĺ�����ϵʽ,��д��x��ȡֵ��Χ����)������ص����ֵ��������
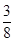 ƽ�����ף�
ƽ�����ף�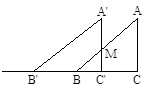
(1) a=4��b=3��(2)����3����ص����ֵ��������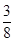 ƽ�����ס�
ƽ�����ס�
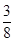 ƽ�����ס�
ƽ�����ס���������Ҫ�ǿ����˺����뷽�����⣬�Լ������ε����Ƶ������ְ�����������������ۺ����á�
��1���ߡ�ABC��Rt����BC=a��AC=b��AB=5 ��a>b��
��a��b�Ƿ��̵�����
��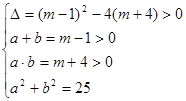 ���������õ�m��ֵ���������õ�a,b��ֵ��
���������õ�m��ֵ���������õ�a,b��ֵ��
��2����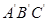 ��1����/����ٶ���BC����ֱ�������ƶ���
��1����/����ٶ���BC����ֱ�������ƶ���
��x���BB��=x ��BC��=4-x
��C��M��AC ���BC��M�ס�BCA ��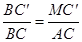 ��
��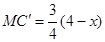
��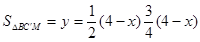 ��
�� ��������ʾ�õ���
��������ʾ�õ���
��:(1)�ߡ�ABC��Rt����BC=a��AC=b��AB=5 ��a>b��
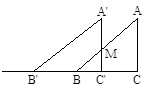
��a��b�Ƿ��̵�����
��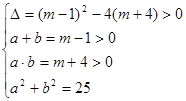 ��(a+b)2-2ab=25
��(a+b)2-2ab=25
(m-1)2-2(m+4)=25 �Ƴ� (m-8)(m+4)=0
��m1=8 m2=-4 ������m=-4��������ȥ�� ��m=8
��x2-7x+12=0 x1=3 x2=4 ��a=4��b=3 ��������6��
(2) �ߡ�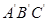 ��1����/����ٶ���BC����ֱ�������ƶ���
��1����/����ٶ���BC����ֱ�������ƶ���
��x���BB��=x ��BC��=4-x
��C��M��AC ���BC��M�ס�BCA ��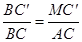 ��
��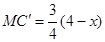
��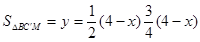 ��
��
��y= (0
(0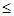 x
x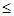 4) ��y=
4) ��y=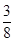 ʱ
ʱ  =
=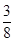
��ã�x1=3 x2=5(������ȥ)
�ྭ��3����ص����ֵ��������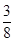 ƽ�����ס�
ƽ�����ס�
��1���ߡ�ABC��Rt����BC=a��AC=b��AB=5 ��a>b��
��a��b�Ƿ��̵�����
��
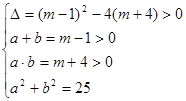 ���������õ�m��ֵ���������õ�a,b��ֵ��
���������õ�m��ֵ���������õ�a,b��ֵ����2����
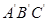 ��1����/����ٶ���BC����ֱ�������ƶ���
��1����/����ٶ���BC����ֱ�������ƶ�����x���BB��=x ��BC��=4-x
��C��M��AC ���BC��M�ס�BCA ��
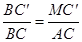 ��
��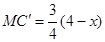
��
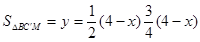 ��
�� ��������ʾ�õ���
��������ʾ�õ�����:(1)�ߡ�ABC��Rt����BC=a��AC=b��AB=5 ��a>b��
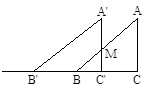
��a��b�Ƿ��̵�����
��
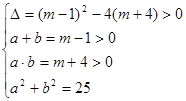 ��(a+b)2-2ab=25
��(a+b)2-2ab=25(m-1)2-2(m+4)=25 �Ƴ� (m-8)(m+4)=0
��m1=8 m2=-4 ������m=-4��������ȥ�� ��m=8
��x2-7x+12=0 x1=3 x2=4 ��a=4��b=3 ��������6��
(2) �ߡ�
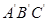 ��1����/����ٶ���BC����ֱ�������ƶ���
��1����/����ٶ���BC����ֱ�������ƶ�����x���BB��=x ��BC��=4-x
��C��M��AC ���BC��M�ס�BCA ��
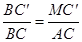 ��
��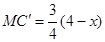
��
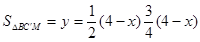 ��
��
��y=
 (0
(0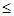 x
x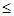 4) ��y=
4) ��y=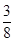 ʱ
ʱ  =
=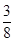
��ã�x1=3 x2=5(������ȥ)
�ྭ��3����ص����ֵ��������
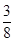 ƽ�����ס�
ƽ�����ס� 
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
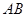 ����
���� ��O��һ��
��O��һ��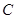 ����
����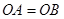 ��
��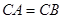 ����O��ֱ��
����O��ֱ��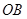 ��
��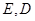 .
.
 ��O�İ뾶Ϊ3����
��O�İ뾶Ϊ3����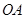 �ij�.
�ij�.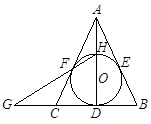
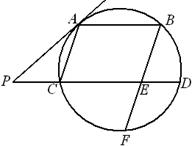
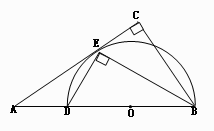
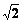 ����BC�ij���
����BC�ij���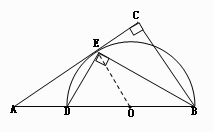
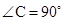 , BEƽ�֡�ABC��AC�ڵ�E�� ��D��AB�ϣ�
, BEƽ�֡�ABC��AC�ڵ�E�� ��D��AB�ϣ�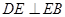 ��
��
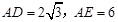 ����EC�ij���
����EC�ij���
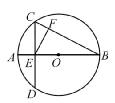
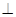 AB�ڵ�D����CD= ��
AB�ڵ�D����CD= ��