题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上的最小值为0,求
上的最小值为0,求![]() 的值;
的值;
(3)当![]() 时,若函数
时,若函数![]() 在
在![]() 上既有最大值又有最小值,且
上既有最大值又有最小值,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递减区间为![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)将![]() 代入函数解析式,去掉绝对值符号,将函数写出分段函数的形式,结合二次函数的单调性,写出函数的单调递减区间;
代入函数解析式,去掉绝对值符号,将函数写出分段函数的形式,结合二次函数的单调性,写出函数的单调递减区间;
(2)将函数解析式化为分段函数的形式,对![]() 的范围进行讨论,从而确定函数的最小值点,相互对照,求得结果;
的范围进行讨论,从而确定函数的最小值点,相互对照,求得结果;
(3)首先根据题意,判断出函数在区间上存在最值的条件,利用恒成立,转化得出对应的不等关系,进而求得其范围.
(1)当![]() 时,
时,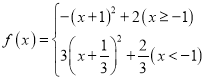
由二次函数单调性知![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递减,
单调递减,
∴![]() 的单调递减区间为
的单调递减区间为![]()
(2)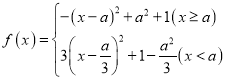
当![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() 单调递减,
单调递减,
(i)当![]() 即
即![]() 时,
时,![]()
∴![]() (舍去)
(舍去)
(ii)由![]() 得
得![]()
当![]() ,即
,即![]() 时,
时,![]()
∴![]() ,符合题意.
,符合题意.
(iii)当![]() ,即
,即![]() 时,
时,![]()
∴![]() ,符合题意.
,符合题意.
综上所述,![]() 或
或![]() .
.
(3)当![]() 时,由
时,由![]() ,可知
,可知![]()
由![]() 可知
可知![]()
要使![]() 恒成立
恒成立
∵![]()
又∵![]()
∴![]() ,∴
,∴![]()
∴![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
数学成绩分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150] |
人数 | 60 | 90 | 300 | x | 160 |
(Ⅰ)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率;
(Ⅱ)作出频率分布直方图,并估计该学校本次考试的数学平均分.(同一组中的数据用该组区间的中点值作代表)
【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。