题目内容
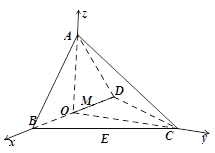
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]()

(Ⅰ)求证:![]() 平面BCD;
平面BCD;
(Ⅱ)求点E到平面ACD的距离.
【答案】(Ⅰ)详见解析 (Ⅱ)![]()
【解析】
试题(Ⅰ)要证明![]() 平面BCD,需要证明
平面BCD,需要证明![]() ,
,![]() ,证明时主要是利用已知条件中的线段长度满足勾股定理和等腰三角形三线合一的性质(Ⅱ)中由已知条件空间直角坐标系容易建立,因此可采用空间向量求解,以
,证明时主要是利用已知条件中的线段长度满足勾股定理和等腰三角形三线合一的性质(Ⅱ)中由已知条件空间直角坐标系容易建立,因此可采用空间向量求解,以![]() 为坐标原点,以
为坐标原点,以![]() 方向为
方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
求出平面![]() 的法向量
的法向量![]() 和斜线的方向向量
和斜线的方向向量![]() ,代入公式
,代入公式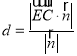 计算
计算
试题解析:(Ⅰ)证明:![]() 为
为![]() 的中点,
的中点,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]()
![]() ,
,![]() ,
,
![]() ,
,![]() 均在平面
均在平面![]() 内,
内,![]() 平面
平面![]()
(Ⅱ)方法一:以![]() 为坐标原点,以
为坐标原点,以![]() 方向为
方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向建立空间直角坐标系,则
轴正方向建立空间直角坐标系,则![]() ,
,
![]()
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则![]()
![]() ,
,![]()
![]()
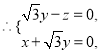 取
取![]()
![]() ,
,
![]() ,则点
,则点![]() 到平面
到平面![]() 的距离为
的距离为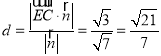
方法二:设点![]() 在
在![]() 上,且
上,且![]() ,连
,连![]() ,
,
![]()
![]() 为
为![]() 的中点,
的中点,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,且交线为
,且交线为![]()
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]()
![]() 分别为
分别为![]() 的中点,则
的中点,则![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 点到平面
点到平面![]() 的距离即
的距离即![]() ,
,
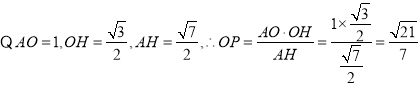
故点![]() 到平面
到平面![]() 的距离为
的距离为![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:

![]()
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中 .
.
【题目】2017年被称为“新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进.辽宁地区也将于2020年开启新高考模式,今年秋季入学的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为自己将来高考“语数外+3”新高考方案中的“3”.某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程组合选择一种学习.模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物政历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | …… | 40人 | …… | …… |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | …… | …… | …… | …… | …… | …… | 200人 |
为了解学生成绩与学生模拟选课之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析。
(1)样本中选择组合6号“物生历”的有多少人?样本中同时选择学习物理和历史的有多少人?
(2)从样本选择学习物理且学习历史的学生中随机抽取3人,求这3人中至少有2人还要学习生物的概率。

