题目内容
7.不等式|x+1|+|2x-1|<3的解集为(-1,1).分析 把原不等式去掉绝对值,转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.
解答 解:不等式|x+1|+|2x-1|<3等价于{x<−1−x−1+1−2x<3①,或{−1≤x<12x+1+1−2x<3②,或{x≥12x+1+2x−1<3③.
解①求得x∈∅,解②求得-1<x<12,解③求得12≤x<1,
综合可得,原不等式的解集为(-1,1),
故答案为:(-1,1).
点评 本题主要考查绝对值的意义,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,属于基础题.

练习册系列答案
相关题目
17.甲、乙两人在一次设计比赛中各射靶5次,两人成绩的条形图如图所示,则( )
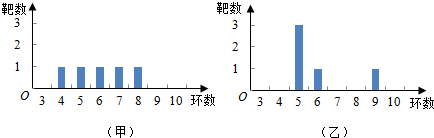

| A. | 甲的成绩的平均数小于乙的成绩的平均数 | |
| B. | 甲的成绩的极差小于乙的成绩的极差 | |
| C. | 甲的成绩的方差小于乙的成绩的方差 | |
| D. | 甲的成绩的中位数等于乙的成绩的中位数 |