题目内容
15.以半径为R的半球的球心O为顶点的圆锥内接于半球,且圆锥底面平行于半球大圆面,则圆锥体积的最大值是$\frac{2\sqrt{3}}{27}$πR3.分析 设圆锥高为h,则底面半径为$\sqrt{{R}^{2}-{h}^{2}}$,可得圆锥体积,利用导数的方法求出圆锥体积的最大值.
解答 解:设圆锥高为h,则底面半径为$\sqrt{{R}^{2}-{h}^{2}}$,
∴圆锥体积V=$\frac{1}{3}π({R}^{2}-{h}^{2})h$,
∴V′=$\frac{1}{3}π({R}^{2}-3{h}^{2})$,
∴R=$\sqrt{3}$h时,圆锥体积的最大值是$\frac{2\sqrt{3}}{27}$πR3.
故答案为:$\frac{2\sqrt{3}}{27}$πR3
点评 本题考查圆锥体积的最大值,考查学生的计算能力,正确表示圆锥体积是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.从3男2女五人中选出3人组成一个工作小组,则至少含有1男1女的不同选法为( )
| A. | 18 | B. | 9 | C. | 7 | D. | 6 |
20.若${C}_{4}^{x}$+${C}_{4}^{x+1}$=5,则x=( )
| A. | 0或3 | B. | 0 | C. | 3 | D. | 2 |
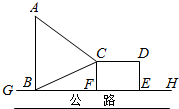 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm