题目内容
16.(1)已知角a的顶点在原点,始边与x轴的非负半轴重合,终边经过点P(-3,$\sqrt{3}$),求$\frac{tan(-a)+sin(\frac{π}{2}+a)}{cos(π-a)sin(-π-a)}$的值.
(2)在△ABC中,sinA=$\frac{5}{13}$,cosB=$\frac{3}{5}$,求cosC的值.
分析 (1)根据题意分别求得sinα,cosα和tanα的值,利用诱导公式进行化简,进而求得答案.
(2)求得sinB,cosA的值,进而利用两角和公式求得答案.
解答 解:(1)因为角α的终边经过点P(-3,$\sqrt{3}$)
所以r=|OP|=$\sqrt{(-\sqrt{3})^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,
所以sinα=$\frac{1}{2}$,cosα=-$\frac{\sqrt{3}}{2}$,tanα=-$\frac{\sqrt{3}}{3}$,
原式=$\frac{-tanα+cosα}{-cosαsinα}$=$\frac{1}{co{s}^{2}α}$-$\frac{1}{sinα}$=$\frac{4}{3}$-2=-$\frac{2}{3}$
(2)因为在△ABC 中,sinA=$\frac{5}{13}$,cosB=$\frac{3}{5}$
所以sinB=$\frac{4}{5}$>$\frac{5}{13}$,
所以B>A,得出cosA=$\frac{12}{13}$.
∴cosC=-cos(A+B)=sinAsinB-cosAcosB=$\frac{5}{13}$×$\frac{4}{5}$-$\frac{12}{13}$×$\frac{3}{5}$=-$\frac{16}{65}$.
点评 本题主要考查了诱导公式,同角三角函数关系化简求值.解题过程中特别注意三角函数符号的判断.

练习册系列答案
相关题目
11.设a=2sin13°cos13°,b=$\frac{2tan76°}{1+ta{n}^{2}76°}$,c=$\sqrt{\frac{1-cos50°}{2}}$,则有( )
| A. | c<a<b | B. | a<b<c | C. | b<c<a | D. | a<c<b |
1.A、B、C、D分别是复数z1,z2,z3=z1+z2,z4=z1-z2在复平面内对应的点,O是原点,若|z1|=|z2|,则△COD一定是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
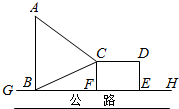 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm