题目内容
17.设x是纯虚数,y是实数,且2x-1+i=y-(3-y)i,则|x+y|=$\frac{7}{2}$.分析 设x=ai(a∈R,且a≠0).代入2x-1+i=y-(3-y)i,可得2ai-1+i=y-(3-y)i,利用复数相等、模的计算公式即可得出.
解答 解:设x=ai(a∈R,且a≠0).
∵2x-1+i=y-(3-y)i,
∴2ai-1+i=y-(3-y)i,
∴-1=y,2a+1=-(3-y),
解得y=-1,a=-$\frac{5}{2}$.
x+yi=$-\frac{5}{2}i$-i=-$\frac{7i}{2}$.
则|x+y|=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 本题考查了复数相等、模的计算公式,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
8.下列求导运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | B. | (3x)′=3xlog3e | ||
| C. | (log23x)′=$\frac{1}{xln2}$ | D. | (x2cos x)′=-2xsin x |
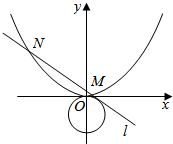 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).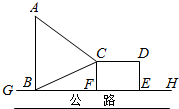 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm