题目内容
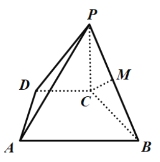
【题目】如图所示,四棱锥P﹣ABCD中,PC⊥底面ABCD,PC=CD=2,E为AB的中点,底面四边形ABCD满足∠ADC=∠DCB=90°,AD=1,BC=3.
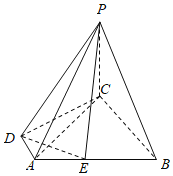
(Ⅰ)求证:平面PDE⊥平面PAC;
(Ⅱ)求直线PC与平面PDE所成角的正弦值;
(Ⅲ)求二面角D﹣PE﹣B的余弦值.
【答案】(Ⅰ)证明见解析(Ⅱ)![]() .(Ⅲ)﹣
.(Ⅲ)﹣![]() .
.
【解析】
(Ⅰ)由题知![]() ,如图以点
,如图以点![]() 为原点,直线
为原点,直线![]() 分别为
分别为![]() 轴,建立空间直角坐标系,计算
轴,建立空间直角坐标系,计算![]() ,证明
,证明![]() ,从而
,从而![]() 平面PAC,即可得证;
平面PAC,即可得证;
(Ⅱ)求解平面PDE的一个法向量![]() ,计算
,计算![]() ,即可得直线PC与平面PDE所成角的正弦值;
,即可得直线PC与平面PDE所成角的正弦值;
(Ⅲ)求解平面PBE的一个法向量![]() ,计算
,计算![]() ,即可得二面角D﹣PE﹣B的余弦值.
,即可得二面角D﹣PE﹣B的余弦值.
(Ⅰ)![]() PC⊥底面ABCD,
PC⊥底面ABCD,![]() ,
,
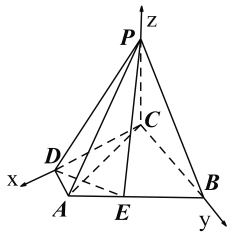
如图以点![]() 为原点,直线
为原点,直线![]() 分别为
分别为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,![]() 平面PAC,
平面PAC,
![]() 平面PDE,
平面PDE,![]() 平面PDE⊥平面PAC;
平面PDE⊥平面PAC;
(Ⅱ)设![]() 为平面PDE的一个法向量,
为平面PDE的一个法向量,
又![]() ,
,
则
![]() ,取
,取![]() ,得
,得![]()
 ,
,
![]() 直线PC与平面PDE所成角的正弦值
直线PC与平面PDE所成角的正弦值![]() ;
;
(Ⅲ)设![]() 为平面PBE的一个法向量,
为平面PBE的一个法向量,
又![]()
则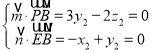 ,取
,取![]() ,得
,得![]() ,
,
 ,
,
![]() 二面角D﹣PE﹣B的余弦值﹣
二面角D﹣PE﹣B的余弦值﹣![]() .
.

【题目】2017年诺贝尔奖陆续揭晓,北京时间10月2日17:30首先公布了生理学和医学奖,获奖者分别是三位美国科学家霍尔(Jeffrey C. Hall)、罗斯巴什(Michael Rosbash)和杨(Michael W. Ymmg),以表彰他们“发现控制生理节律的分子机制”.通过他们的研究成果发现,人类每天睡眠时间在7-9小时为最佳状态.从某大学随机挑选了100名学生(男生、女生各50名)做睡眠时间统计调查,调查结果如下:
睡眠时间(小时) |
|
|
|
|
|
|
|
男生 | 5 | 6 | 12 | 12 | 8 | 5 | 2 |
女生 | 0 | 2 | 6 | 18 | 12 | 10 | 2 |
请根据上面表格回答下列问题:
(1)请分别估计出该校男生和女生的平均睡眠时间;