题目内容
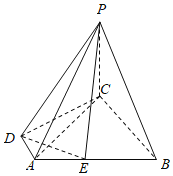
【题目】如图,在四棱锥P-ABCD中,PC⊥平面ABCD,点M为PB中点,底面ABCD为梯形,AB∥CD,AD⊥CD,AD=CD=PC=![]() AB.
AB.
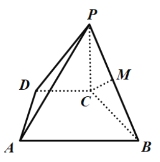
(1)证明:CM∥平面PAD;
(2)若四棱锥P-ABCD的体积为4,求点M到平面PAD的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)利用线面平行判定定理,结合中位线定理,即可证明;
(2)设![]() ,则
,则![]() ,由四棱锥
,由四棱锥![]() 的体积得出
的体积得出![]() ,由
,由![]() 平面
平面![]() 知,点
知,点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,过点
的距离,过点![]() 作
作![]() ,垂足于点
,垂足于点![]() ,利用线面垂直的判定定理以及性质得出
,利用线面垂直的判定定理以及性质得出![]() 平面
平面![]() ,从而得出点M到平面PAD的距离.
,从而得出点M到平面PAD的距离.
(1)取![]() 中点为
中点为![]() ,连接
,连接![]()

![]() 为
为![]() 中点,
中点,![]() 且
且![]()
又![]()
![]() ,且
,且![]()
![]() 且
且![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]()
(2)设![]() ,则
,则![]()
由四边形![]() 是直角梯形,
是直角梯形,![]() 平面
平面![]()
得四棱锥![]() 的体积为
的体积为![]()
由![]() 平面
平面![]() 知,点
知,点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离
的距离
过点![]() 作
作![]() ,垂足于点
,垂足于点![]()

![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
由![]() 知,
知,![]()
![]() 到平面
到平面![]() 的距离等于
的距离等于![]()

练习册系列答案
相关题目
【题目】某快递公司有两种发放薪水的方案:
方案一:底薪1800元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为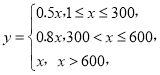
方案二:底薪2000元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为![]()
以下该公司某职工小甲在2019年9月份(30天)送快递的数据,
日送快递单数 | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)从小甲日送快递单数大于15的六天中抽取两天,求这两天他送的快递单数恰好都为16单的概率.
(2)请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案,并说明理由.