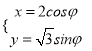题目内容
【题目】已知椭圆![]() ,点
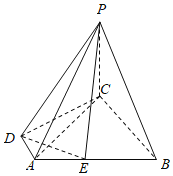
,点![]() 为半圆
为半圆![]() 上一动点,若过
上一动点,若过![]() 作椭圆
作椭圆![]() 的两切线分别交
的两切线分别交![]() 轴于
轴于![]() 、
、![]() 两点.
两点.
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)分两种情况讨论:①两切线![]() 、
、![]() 中有一条切线斜率不存在时,求出两切线的方程,验证结论成立;②两切线
中有一条切线斜率不存在时,求出两切线的方程,验证结论成立;②两切线![]() 、
、![]() 的斜率都存在,可设切线的方程为
的斜率都存在,可设切线的方程为![]() ,将该直线的方程与椭圆的方程联立,由
,将该直线的方程与椭圆的方程联立,由![]() 可得出关于
可得出关于![]() 的二次方程,利用韦达定理得出两切线的斜率之积为
的二次方程,利用韦达定理得出两切线的斜率之积为![]() ,进而可得出结论;
,进而可得出结论;
(2)求出点![]() 、
、![]() 的坐标,利用两点间的距离公式结合韦达定理得出
的坐标,利用两点间的距离公式结合韦达定理得出 ,换元
,换元![]() ,可得出
,可得出 ,利用二次函数的基本性质可求得
,利用二次函数的基本性质可求得![]() 的取值范围.
的取值范围.
(1)由于点![]() 在半圆
在半圆![]() 上,则
上,则![]() .
.
①当两切线![]() 、
、![]() 中有一条切线斜率不存在时,可求得两切线方程为
中有一条切线斜率不存在时,可求得两切线方程为![]() ,
,![]() 或
或![]() ,
,![]() ,此时
,此时![]() ;
;
②当两切线![]() 、
、![]() 的斜率都存在时,设切线的方程为
的斜率都存在时,设切线的方程为![]() (
(![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ),
),
![]()
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
综上所述,![]() ;
;
(2)根据题意得 、
、 ,
,

 ,
,
令![]() ,则
,则 ,
,
所以,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
因此,![]() 的取值范围是
的取值范围是![]() .
.

【题目】第十四届全国冬季运动会召开期间,某校举行了“冰上运动知识竞赛”,为了解本次竞赛成绩情况,从中随机抽取部分学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
(1)求![]() 、
、![]() 、
、![]() 的值及随机抽取一考生其成绩不低于70分的概率;
的值及随机抽取一考生其成绩不低于70分的概率;
(2)若从成绩较好的3、4、5组中按分层抽样的方法抽取5人参加“普及冰雪知识”志愿活动,并指定2名负责人,求从第4组抽取的学生中至少有一名是负责人的概率.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 15 | 0.15 |
第2组 |
| 35 | 0.35 |
第3组 |
| b | 0.20 |
第4组 |
| 20 |
|
第5组 |
| 10 | 0.1 |
合计 |
| 1.00 | |
【题目】某快递公司有两种发放薪水的方案:
方案一:底薪1800元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为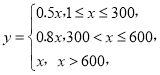
方案二:底薪2000元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为![]()
以下该公司某职工小甲在2019年9月份(30天)送快递的数据,
日送快递单数 | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)从小甲日送快递单数大于15的六天中抽取两天,求这两天他送的快递单数恰好都为16单的概率.
(2)请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案,并说明理由.