题目内容
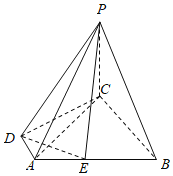
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 为棱长为2的菱形,
为棱长为2的菱形,![]() ,
,![]() ,
,![]() .
.

(1)求证:面![]() 面
面![]() ;
;
(2)求直线![]() 与面
与面![]() 所成角.
所成角.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,通过菱形的性质得出
,通过菱形的性质得出![]() ,
,![]() ,得出
,得出![]() 为等边三角形,根据三边关系得出
为等边三角形,根据三边关系得出![]() ,则
,则![]() ,而
,而![]() ,根据线面垂直的判定定理得出
,根据线面垂直的判定定理得出![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,从而可证出平面
,从而可证出平面![]() 平面
平面![]() ;
;
(2)由面面垂直的性质得出![]() 面
面![]() ,则
,则![]() 即为
即为![]() 与面
与面![]() 所成角,通过几何法求得
所成角,通过几何法求得![]() ,即可求出直线
,即可求出直线![]() 与面
与面![]() 所成角.
所成角.
解:(1)证明:连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,
因为![]() 为菱形,
为菱形,![]() ,
,
所以![]() ,
,![]() ,
,
则![]() 为等边三角形,即可得
为等边三角形,即可得![]() ,
,
又![]() ,
,
所以在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
又知![]() ,
,![]() ,
,
且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
即平面![]() 平面
平面![]() .
.
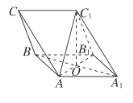
(2)由(1)知平面![]() 平面
平面![]() ,
,
因为![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 面
面![]() ,
,
则![]() 即为
即为![]() 与面
与面![]() 所成角,
所成角,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
所以直线![]() 与面
与面![]() 所成角为
所成角为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】随着中美贸易战的不断升级,越来越多的国内科技巨头加大了科技研发投入的力度.中华技术有限公司拟对“麒麟”手机芯片进行科技升级,根据市场调研与模拟,得到科技升级投入x(亿元与科技升级直接收益y(亿元)的数据统计如下:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
x | 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
y | 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
当![]() 时,建立了y与x的两个回归模型:模型①:
时,建立了y与x的两个回归模型:模型①:![]() ;模型②:
;模型②:![]() ;当
;当![]() 时,确定y与x满足的线性回归方程为
时,确定y与x满足的线性回归方程为![]() .
.
(1)根据下列表格中的数据,比较当![]() 时模型①、②的相关指数
时模型①、②的相关指数![]() 的大小,并选择拟合精度更高、更可靠的模型,预测对“麒麟”手机芯片科技升级的投入为17亿元时的直接收益.
的大小,并选择拟合精度更高、更可靠的模型,预测对“麒麟”手机芯片科技升级的投入为17亿元时的直接收益.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
(附:刻画回归效果的相关指数 ,
,![]() )
)
(2)为鼓励科技创新,当科技升级的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,比较科技升级投入17亿元与20亿元时公司实际收益的大小.
(附:用最小二乘法求线性回归方程![]() 的系数:
的系数: ,
,![]() )
)
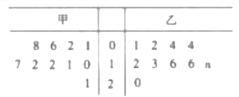
(3)科技升级后,“麒麟”芯片的效率X大幅提高,经实际试验得X大致服从正态分布![]() .公司对科技升级团队的奖励方案如下:若芯片的效率不超过50%,不予奖励:若芯片的效率超过50%,但不超过53%,每部芯片奖励2元;若芯片的效率超过53%,每部芯片奖励4元记为每部芯片获得的奖励,求
.公司对科技升级团队的奖励方案如下:若芯片的效率不超过50%,不予奖励:若芯片的效率超过50%,但不超过53%,每部芯片奖励2元;若芯片的效率超过53%,每部芯片奖励4元记为每部芯片获得的奖励,求![]() (精确到0.01).
(精确到0.01).
(附:若随机变量![]() ,则
,则![]() ,
,![]() )
)