题目内容
20.如图1,在直角梯形ABCD中,∠A=∠B=90°,AD=2,BC=3,EF∥AB,且AE=1,M,N分别是FC,CD的中点.将梯形ABCD沿EF折起,使得BM=1,连接AD,BC,AC得到(图2)所示几何体.
(Ⅰ)证明:BC⊥平面ABFE;
(Ⅱ)证明:AF∥平面BMN.
分析 (Ⅰ)只要证明BC与平面ABFE内的AB,BF垂直即可;
(Ⅱ)连接DF,只要证明DF∥MN,AD∥BM,两腰两个平面平行的判定定理可得.
解答 证明:(Ⅰ)由已知得到BF=BM=F=,∴∠BFC=60°,由余弦定理得到BC=$\sqrt{3}$,∴BC2+BF2=FC2,∴BC⊥FB,
又AB⊥BC,∴BC⊥平面ABFE;
(Ⅱ)连接DF,∵M,N是FC,CD的中点,∴MN∥DF,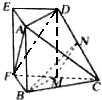
∵DE∥FC,AE∥FB,
∴平面AED∥平面BFM,并且,∠A=∠B=90°,EF∥AB,
∴几何体AED-BFM是正三棱柱,∴AB∥DM∴AD∥BM,
∴平面ADF∥平面BMN.
又AF?平面ADF,
∴AF∥平面BMN.
点评 本题考查了线面垂直和线面平行的判定定理和性质定理的运用;关键是熟练掌握定理成立的条件,正确运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
12.下面是高考第一批录取的一份志愿表:
现有4所重点院校,每所院校有3个专业是你较为满意的选择,如果从中任选3所随意填报,表格填满且规定学校没有重复,同一学校的专业也没有重复的话,不同的填写方法的种数是多少?
| 志愿 | 第一志愿 | 第二志愿 | 第三志愿 |
| 学校 | 1 | 2 | 3 |
| 专业 | 第1专业 | 第1专业 | 第1专业 |
| 第2专业 | 第2专业 | 第2专业 |
 如图,在四棱柱P-ABCD中,底面是边长为2的正方形,侧棱PA⊥底面ABCD,PA=2,M,N分别为AD,BC的中点.
如图,在四棱柱P-ABCD中,底面是边长为2的正方形,侧棱PA⊥底面ABCD,PA=2,M,N分别为AD,BC的中点.




 如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为4的棱形,∠ABC=60°,AC与BD交于点O,M、N分别是OC、PD的中点,异面直线BD与AN所成角的余弦值为$\frac{{2\sqrt{3}}}{5}$.
如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为4的棱形,∠ABC=60°,AC与BD交于点O,M、N分别是OC、PD的中点,异面直线BD与AN所成角的余弦值为$\frac{{2\sqrt{3}}}{5}$.