题目内容
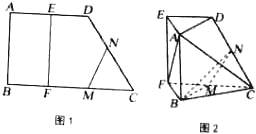
8.如图1,在直角梯形ABCD中,∠A=∠B=90°,AD=AB=2,BC=3,EF∥AB,且AE=1,M,N分别是FC,CD的中点.将梯形ABCD沿EF折起,使得BC=$\sqrt{3}$,连接AD,BC,AC得到(图2)所示几何体.
(Ⅰ)证明:AF∥平面BMN;
(Ⅱ)求二面角B-AC-D的余弦值.
分析 (Ⅰ)取AC中点P,连结PB、PN、PM,连结DM.通过四边形ABMD是平行四边形及线面平行的判定定理即得结论;
(Ⅱ)以B为坐标原点,建立空间直角坐标系B-xyz,则所求值即为平面ADC的法向量与平面ABC的一个法向量的夹角的余弦值的绝对值的相反数,计算即可.
解答  (Ⅰ)证明:取AC中点P,连结PB、PN、PM.
(Ⅰ)证明:取AC中点P,连结PB、PN、PM.
则PN∥AD,AF∥PM.
连结DM,则DM∥EF,DM=EF,
由题意知EF∥AB,EF=AB,
∴DM∥AB,DM=AB,
∴四边形ABMD是平行四边形,
∴MB∥AD,∴MB∥NP,
∴B、M、N、P共面,
∴PM?平面BMN,
又∵AF?平面BMN,
∴AF∥平面BMN;
(Ⅱ) 解:由题意知EF⊥FB,EF⊥FC,∴EF⊥平面FBC,
解:由题意知EF⊥FB,EF⊥FC,∴EF⊥平面FBC,
∵EF∥AB,∴AB⊥平面FBC,
又BC2+BF2=FC2,∴BC⊥BF,
以B为坐标原点,建立空间直角坐标系B-xyz如图,
则B(0,0,0),A(0,0,2),C($\sqrt{3}$,0,0),D($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,2),
∴$\overrightarrow{AC}$=($\sqrt{3}$,0,-2),$\overrightarrow{AD}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),
设平面ADC的法向量为$\overrightarrow{m}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{AD}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{\sqrt{3}x-2z=0}\\{\sqrt{3}x+y=0}\end{array}\right.$,
取x=1,得$\overrightarrow{m}$=(1,-$\sqrt{3}$,$\frac{\sqrt{3}}{2}$),
又平面ABC的一个法向量为$\overrightarrow{n}$=(0,1,0),
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=-$\frac{2\sqrt{57}}{19}$,
由图可知二面角B-AC-D为钝角,
∴二面角B-AC-D的余弦值为-$\frac{2\sqrt{57}}{19}$.
点评 本题考查线面平行的判定,求二面角的三角函数值,涉及到勾股定理及向量数量积运算等知识,注意解题方法的积累,属于中档题.

| A. | {x|2<x≤3} | B. | {3} | C. | {2,3} | D. | {x|-1≤x<2} |
| A. | 0.477 | B. | 0.628 | C. | 0.954 | D. | 0.977 |
| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
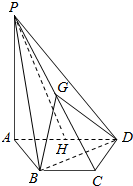 已知在四棱锥P-ABCD中,底面ABCD是等腰梯形,AD∥BC,∠BAD=60°,PA⊥平面ABCD,AD=2,BC=1,PA=2$\sqrt{2}$,H,G分别为AD,PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是等腰梯形,AD∥BC,∠BAD=60°,PA⊥平面ABCD,AD=2,BC=1,PA=2$\sqrt{2}$,H,G分别为AD,PC的中点.