题目内容
已知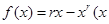
＞0），其中r是区间（0，1）上的常数，则
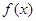的单调增区间为 。
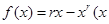＞0），其中r是区间（0，1）上的常数，则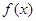的单调增区间为 。（1，+
）。
）。因为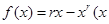＞0），其中r是区间（0，1）上的常数，那么可知
，令f’(x)>0,可知其增区间为（1，+）。
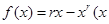＞0），其中r是区间（0，1）上的常数，那么可知，令f’(x)>0,可知其增区间为（1，+）。
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
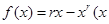＞0），其中r是区间（0，1）上的常数，则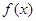的单调增区间为 。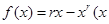）。＞0），其中r是区间（0，1）上的常数，那么可知，令f’(x)>0,可知其增区间为（1，+）。阅读快车系列答案
有两个极值点
，且直线
与曲线
相切于
点.
和
为整数时，求过
的切线
过点
，则切线
.
在点
处的切线方程；
时，求函数
的单调区间.
.
与直线
垂直的切线方程；
使曲线
在
点处的切线斜率为
,且
,求实数
的取值范围.
.
，求曲线
在
处切线的斜率；
的单调区间；
，若对任意
，均存在
，使得
，求
的取值范围。
的值；
过原点的切线与函数
的图像有两个交点，试求b的取值范围.
（其中a（米）是车身长,a为常量）,同时
．
时，求机动车车速的变化范围；
，应规定怎样的车速，使机动车每小时流量Q最大．
则
的单调减区间为（ ）
