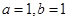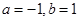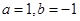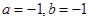题目内容
(本题分12分)
定义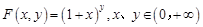 .
.
(Ⅰ)求曲线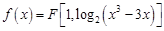 与直线
与直线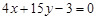 垂直的切线方程;
垂直的切线方程;
(Ⅱ)若存在实数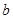 使曲线
使曲线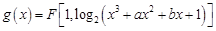 在
在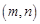 点处的切线斜率为
点处的切线斜率为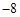 ,且
,且 ,求实数
,求实数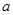 的取值范围.
的取值范围.
定义
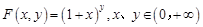 .
.(Ⅰ)求曲线
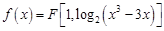 与直线
与直线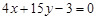 垂直的切线方程;
垂直的切线方程;(Ⅱ)若存在实数
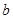 使曲线
使曲线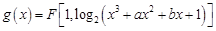 在
在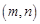 点处的切线斜率为
点处的切线斜率为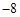 ,且
,且 ,求实数
,求实数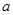 的取值范围.
的取值范围.(1)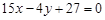 . (2)
. (2)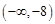 。
。
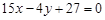 . (2)
. (2)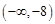 。
。本试题主要是考查了导数的几何意义的运用,以及运用导数求解函数的最值问题的综合运用。
(1)因为所求曲线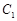 的切线与直线
的切线与直线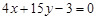 垂直,故令
垂直,故令
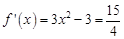 得
得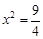 得到
得到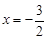 ,进而得到切线方程。
,进而得到切线方程。
(2)函数
令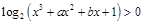 ,得
,得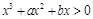
因切点为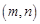 ,故有
,故有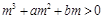 ,构造函数利用导数求解不等式转化为
,构造函数利用导数求解不等式转化为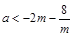 在
在 上有解来解决。
上有解来解决。
解:(1)函数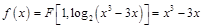 ,
,
依题意令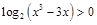 ①, -------------------------2分
①, -------------------------2分
因为所求曲线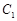 的切线与直线
的切线与直线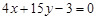 垂直,故令
垂直,故令
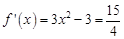 得
得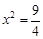 ②,由①②知应取
②,由①②知应取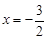 ,得
,得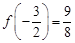 ,切点为
,切点为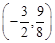 ,
,
所求切线方程是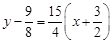 ,即
,即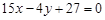 .------------------4分
.------------------4分
(2)函数
令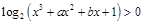 ,得
,得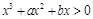
因切点为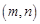 ,故有
,故有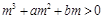 -----------------6分
-----------------6分
又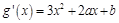 ,依题意有
,依题意有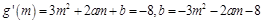
所以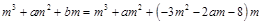
即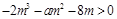 ---------------------8分
---------------------8分
该不等式在 上有解,即
上有解,即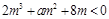 在
在 上有解,
上有解,
转化为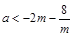 在
在 上有解,-------- -------------10分
上有解,-------- -------------10分
令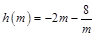 ,则
,则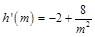 ,在
,在 上恒有
上恒有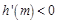
所以函数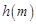 是
是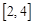 上的减函数,
上的减函数,
其最大值为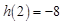 ,所以实数
,所以实数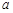 的取值范围是
的取值范围是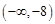 --------------12分
--------------12分
(1)因为所求曲线
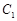 的切线与直线
的切线与直线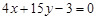 垂直,故令
垂直,故令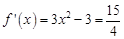 得
得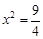 得到
得到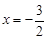 ,进而得到切线方程。
,进而得到切线方程。(2)函数

令
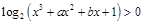 ,得
,得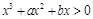
因切点为
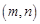 ,故有
,故有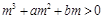 ,构造函数利用导数求解不等式转化为
,构造函数利用导数求解不等式转化为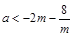 在
在 上有解来解决。
上有解来解决。解:(1)函数
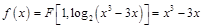 ,
, 依题意令
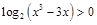 ①, -------------------------2分
①, -------------------------2分因为所求曲线
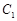 的切线与直线
的切线与直线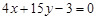 垂直,故令
垂直,故令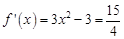 得
得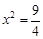 ②,由①②知应取
②,由①②知应取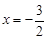 ,得
,得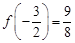 ,切点为
,切点为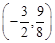 ,
,所求切线方程是
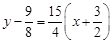 ,即
,即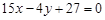 .------------------4分
.------------------4分(2)函数

令
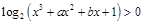 ,得
,得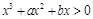
因切点为
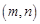 ,故有
,故有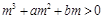 -----------------6分
-----------------6分又
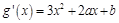 ,依题意有
,依题意有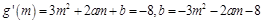
所以
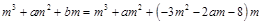
即
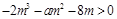 ---------------------8分
---------------------8分该不等式在
 上有解,即
上有解,即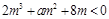 在
在 上有解,
上有解, 转化为
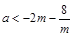 在
在 上有解,-------- -------------10分
上有解,-------- -------------10分令
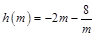 ,则
,则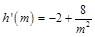 ,在
,在 上恒有
上恒有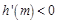
所以函数
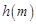 是
是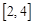 上的减函数,
上的减函数,其最大值为
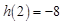 ,所以实数
,所以实数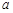 的取值范围是
的取值范围是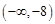 --------------12分
--------------12分
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 .
.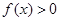 的解集为
的解集为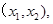 且方程
且方程 的两实根为
的两实根为 .
. ,求
,求 的关系式;
的关系式;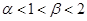 ,求证:
,求证: .
.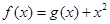 ,曲线
,曲线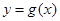 在点
在点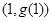 处的切线方程为
处的切线方程为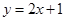 ,则曲线
,则曲线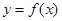 在点
在点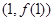 处切线的斜率为
处切线的斜率为 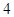



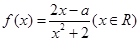
 时,求曲线
时,求曲线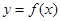 在点
在点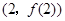 处的切线方程;
处的切线方程;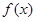 在区间
在区间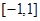 上是增函数,求实数
上是增函数,求实数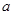 的取值范围
的取值范围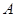 ;
;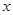 的方程
的方程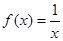 的两个根为
的两个根为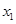 、
、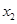 ,若对任意
,若对任意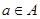 ,
,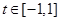 ,不等式
,不等式 恒成立,求
恒成立,求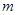 的取值范围.
的取值范围. 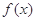 的导函数
的导函数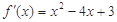 ,则函数
,则函数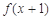 的单调递减区间是 ( )
的单调递减区间是 ( )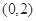
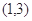
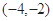
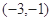
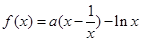
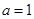 时,求曲线
时,求曲线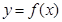 在点
在点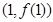 处的切线方程;
处的切线方程;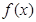 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数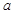 的取值范围;
的取值范围;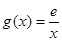 ,若在
,若在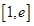 上至少存在一点
上至少存在一点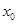 使
使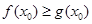 成立,求实数
成立,求实数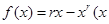 >0),其中r是区间(0,1)上的常数,则
>0),其中r是区间(0,1)上的常数,则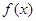 的单调增区间为 。
的单调增区间为 。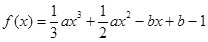 在
在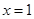 处的切线与
处的切线与 轴平行,若
轴平行,若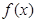 的图象经过四个象限,则实数
的图象经过四个象限,则实数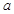 的取值范围是 。
的取值范围是 。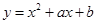 在点
在点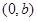 处的切线方程是
处的切线方程是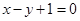 ,则( )
,则( )