题目内容
(本小题14分)已知函数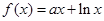
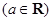 .
.
(1)若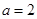 ,求曲线
,求曲线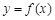 在
在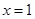 处切线的斜率;
处切线的斜率;
(2)求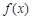 的单调区间;
的单调区间;
(3)设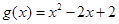 ,若对任意
,若对任意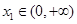 ,均存在
,均存在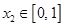 ,使得
,使得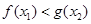 ,求
,求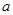 的取值范围。
的取值范围。
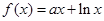
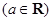 .
.(1)若
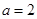 ,求曲线
,求曲线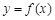 在
在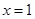 处切线的斜率;
处切线的斜率;(2)求
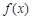 的单调区间;
的单调区间;(3)设
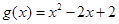 ,若对任意
,若对任意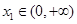 ,均存在
,均存在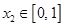 ,使得
,使得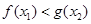 ,求
,求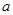 的取值范围。
的取值范围。 (Ⅰ)曲线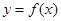 在
在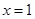 处切线的斜率为
处切线的斜率为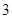 .
.
(Ⅱ)函数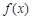 的单调递增区间为
的单调递增区间为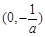 ,单调递减区间为
,单调递减区间为 .
.
(Ⅲ)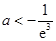 .
.
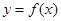 在
在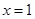 处切线的斜率为
处切线的斜率为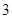 .
.(Ⅱ)函数
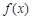 的单调递增区间为
的单调递增区间为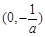 ,单调递减区间为
,单调递减区间为 .
.(Ⅲ)
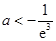 .
. 本试题主要是考查了导数在研究函数中的运用。
(1)本试题主要是考查了导数的几何意义的运用。
(2)求解导数,根据导数的符号来求解函数的单调增减区间。
(3)根据已知条件可知转换为函数的最值之间的关系,进而求解得到结论。
解:(Ⅰ)由已知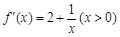 ,…………………………(2分)
,…………………………(2分)
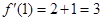 .故曲线
.故曲线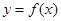 在
在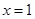 处切线的斜率为
处切线的斜率为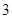 .……………(4分)
.……………(4分)
(Ⅱ)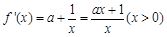 .………………………(5分)
.………………………(5分)
①当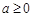 时,由于
时,由于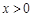 ,故
,故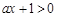 ,
,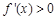
所以,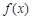 的单调递增区间为
的单调递增区间为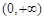 .…………………………(6分)
.…………………………(6分)
②当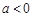 时,由
时,由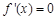 ,得
,得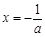 .在区间
.在区间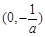 上,
上,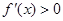 ,在区间
,在区间 上
上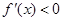 ,
,
所以,函数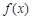 的单调递增区间为
的单调递增区间为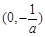 ,单调递减区间为
,单调递减区间为 .…(8分)
.…(8分)
(Ⅲ)由已知,转化为 .……………………………(9分)
.……………………………(9分)
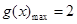 …………………………………………(10分)
…………………………………………(10分)
由(Ⅱ)知,当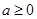 时,
时,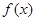 在
在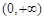 上单调递增,值域为
上单调递增,值域为 ,故不符合题意.
,故不符合题意.
(或者举出反例:存在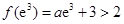 ,故不符合题意.)……………(11分)
,故不符合题意.)……………(11分)
当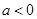 时,
时,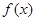 在
在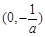 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
故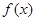 的极大值即为最大值,
的极大值即为最大值,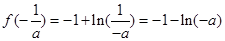 ,……(13分)
,……(13分)
所以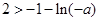 解得
解得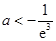 . ……………………(14分)
. ……………………(14分)
(1)本试题主要是考查了导数的几何意义的运用。
(2)求解导数,根据导数的符号来求解函数的单调增减区间。
(3)根据已知条件可知转换为函数的最值之间的关系,进而求解得到结论。
解:(Ⅰ)由已知
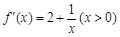 ,…………………………(2分)
,…………………………(2分)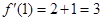 .故曲线
.故曲线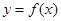 在
在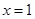 处切线的斜率为
处切线的斜率为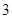 .……………(4分)
.……………(4分)(Ⅱ)
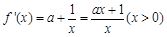 .………………………(5分)
.………………………(5分)①当
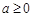 时,由于
时,由于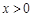 ,故
,故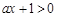 ,
,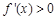
所以,
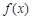 的单调递增区间为
的单调递增区间为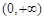 .…………………………(6分)
.…………………………(6分)②当
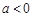 时,由
时,由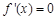 ,得
,得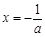 .在区间
.在区间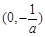 上,
上,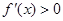 ,在区间
,在区间 上
上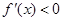 ,
,所以,函数
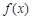 的单调递增区间为
的单调递增区间为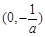 ,单调递减区间为
,单调递减区间为 .…(8分)
.…(8分)(Ⅲ)由已知,转化为
 .……………………………(9分)
.……………………………(9分)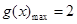 …………………………………………(10分)
…………………………………………(10分)由(Ⅱ)知,当
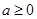 时,
时,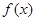 在
在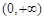 上单调递增,值域为
上单调递增,值域为 ,故不符合题意.
,故不符合题意.(或者举出反例:存在
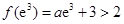 ,故不符合题意.)……………(11分)
,故不符合题意.)……………(11分)当
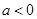 时,
时,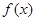 在
在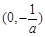 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,故
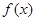 的极大值即为最大值,
的极大值即为最大值,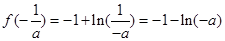 ,……(13分)
,……(13分)所以
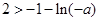 解得
解得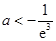 . ……………………(14分)
. ……………………(14分)
练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 的单调递增区间为
的单调递增区间为 ,
, ;
; 取最小值时,点
取最小值时,点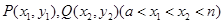 是函数
是函数 图象上的两点,若存在
图象上的两点,若存在 使得
使得 ,求证:
,求证:
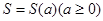 是图1中阴影部分介于平等线
是图1中阴影部分介于平等线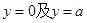 之间的那一部分的面积,则函数
之间的那一部分的面积,则函数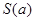 的图象大致为( )
的图象大致为( )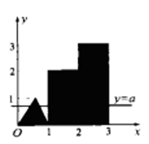
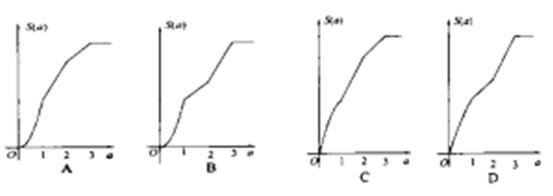
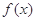 的导函数
的导函数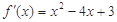 ,则函数
,则函数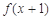 的单调递减区间是 ( )
的单调递减区间是 ( )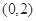
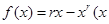 >0),其中r是区间(0,1)上的常数,则
>0),其中r是区间(0,1)上的常数,则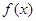 的单调增区间为 。
的单调增区间为 。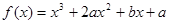 ,
,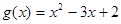 ,其中
,其中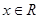 ,a、b为常数,已知曲线
,a、b为常数,已知曲线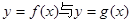 在点(2,0)处有相同的切线
在点(2,0)处有相同的切线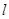 。
。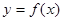 单调区间与极值。
单调区间与极值。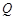 是曲线
是曲线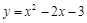 上的两点,且点
上的两点,且点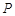 的横坐标是1,点
的横坐标是1,点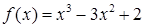 在区间
在区间 上的最大值是_________.
上的最大值是_________.  ,
,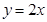 围成的封闭图形的面积为( )
围成的封闭图形的面积为( )