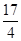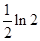题目内容
(本小题满分14分)已知函数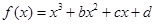 有两个极值点
有两个极值点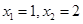 ,且直线
,且直线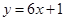 与曲线
与曲线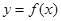 相切于
相切于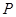 点.
点.
(1) 求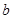 和
和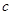
(2) 求函数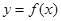 的解析式;
的解析式;
(3) 在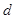 为整数时,求过
为整数时,求过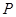 点和
点和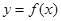 相切于一异于
相切于一异于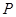 点的直线方程
点的直线方程
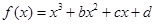 有两个极值点
有两个极值点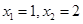 ,且直线
,且直线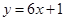 与曲线
与曲线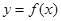 相切于
相切于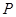 点.
点.(1) 求
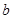 和
和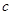
(2) 求函数
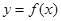 的解析式;
的解析式;(3) 在
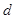 为整数时,求过
为整数时,求过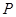 点和
点和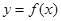 相切于一异于
相切于一异于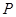 点的直线方程
点的直线方程(1) 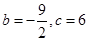 ;
;
(2)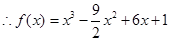 ,或
,或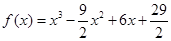 ;
;
(3)切线方程为: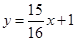 。
。
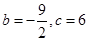 ;
;(2)
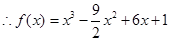 ,或
,或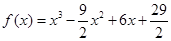 ;
;(3)切线方程为:
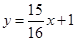 。
。(1)根据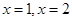 是方程
是方程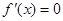 的两个根,借助韦达定理可求出b,c的值.
的两个根,借助韦达定理可求出b,c的值.
(2)设出切点P的坐标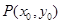 ,根据
,根据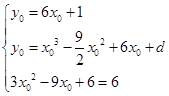 ,可求出切点及d的值,从而确定f(x)的解析式.
,可求出切点及d的值,从而确定f(x)的解析式.
(1)设直线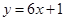 ,和
,和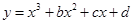 相切于点
相切于点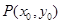
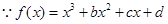
有两个极值点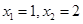 ,于是
,于是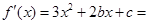
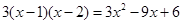
从而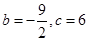 ………………4分
………………4分
(2)又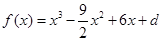 ,且
,且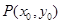 为切点.
为切点.
③则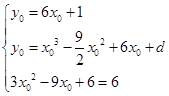 ,由 ③ 求得
,由 ③ 求得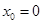 或
或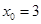 ,由①②联立知
,由①②联立知 .在
.在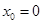 时,
时,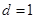 ;在
;在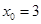 时,
时,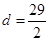
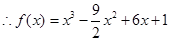 ,或
,或
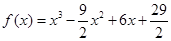 …9分
…9分
(3)当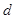 为整数时,
为整数时,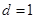 符合条件,此时
符合条件,此时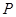 为
为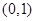 ,设过
,设过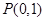 的直线
的直线 和
和

由④⑤及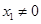 ,可知
,可知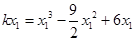 即
即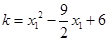 ,再联立⑥可知
,再联立⑥可知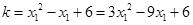 ,又
,又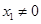 ,
,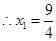 ,此时
,此时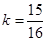 故切线方程为:
故切线方程为: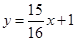 ………………14分
………………14分
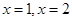 是方程
是方程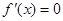 的两个根,借助韦达定理可求出b,c的值.
的两个根,借助韦达定理可求出b,c的值.(2)设出切点P的坐标
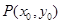 ,根据
,根据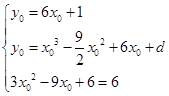 ,可求出切点及d的值,从而确定f(x)的解析式.
,可求出切点及d的值,从而确定f(x)的解析式.(1)设直线
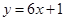 ,和
,和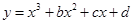 相切于点
相切于点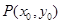
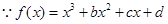
有两个极值点
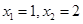 ,于是
,于是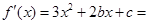
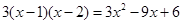
从而
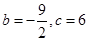 ………………4分
………………4分(2)又
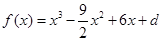 ,且
,且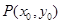 为切点.
为切点.③则
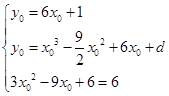 ,由 ③ 求得
,由 ③ 求得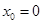 或
或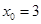 ,由①②联立知
,由①②联立知 .在
.在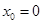 时,
时,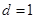 ;在
;在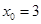 时,
时,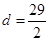
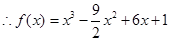 ,或
,或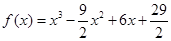 …9分
…9分(3)当
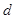 为整数时,
为整数时,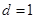 符合条件,此时
符合条件,此时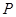 为
为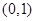 ,设过
,设过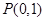 的直线
的直线 和
和
由④⑤及
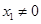 ,可知
,可知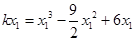 即
即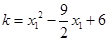 ,再联立⑥可知
,再联立⑥可知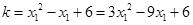 ,又
,又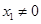 ,
,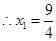 ,此时
,此时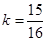 故切线方程为:
故切线方程为: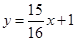 ………………14分
………………14分
练习册系列答案
相关题目
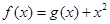 ,曲线
,曲线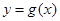 在点
在点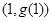 处的切线方程为
处的切线方程为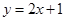 ,则曲线
,则曲线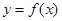 在点
在点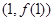 处切线的斜率为
处切线的斜率为 



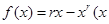 >0),其中r是区间(0,1)上的常数,则
>0),其中r是区间(0,1)上的常数,则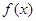 的单调增区间为 。
的单调增区间为 。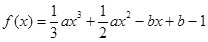 在
在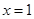 处的切线与
处的切线与 轴平行,若
轴平行,若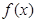 的图象经过四个象限,则实数
的图象经过四个象限,则实数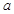 的取值范围是 。
的取值范围是 。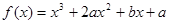 ,
,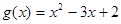 ,其中
,其中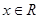 ,a、b为常数,已知曲线
,a、b为常数,已知曲线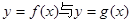 在点(2,0)处有相同的切线
在点(2,0)处有相同的切线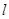 。
。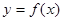 单调区间与极值。
单调区间与极值。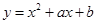 在点
在点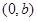 处的切线方程是
处的切线方程是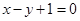 ,则( )
,则( )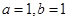
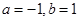
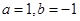
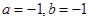
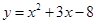 在与直线
在与直线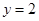 的交点处的切线方程为 .
的交点处的切线方程为 .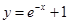 在
在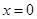 处的切线方程为_____________.
处的切线方程为_____________.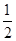 ,x=2,曲线
,x=2,曲线 及x轴所围图形的面积为( )
及x轴所围图形的面积为( )