题目内容
(本小题满分15分)已知点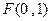 ,一动圆过点
,一动圆过点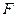 且与圆
且与圆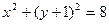 内切.
内切.
(Ⅰ)求动圆圆心的轨迹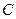 的方程;
的方程;
(Ⅱ)设点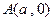 ,点
,点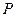 为曲线
为曲线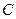 上任一点,求点
上任一点,求点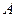 到点
到点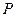 距离的最大值
距离的最大值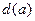 ;
;
(Ⅲ)在 的条件下,设△
的条件下,设△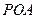 的面积为
的面积为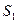 (
(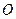 是坐标原点,
是坐标原点,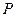 是曲线
是曲线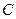 上横坐标为
上横坐标为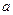 的点),以
的点),以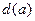 为边长的正方形的面积为
为边长的正方形的面积为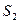 .若正数
.若正数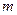 满足
满足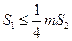 ,问
,问 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
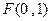 ,一动圆过点
,一动圆过点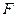 且与圆
且与圆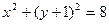 内切.
内切.(Ⅰ)求动圆圆心的轨迹
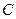 的方程;
的方程;(Ⅱ)设点
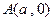 ,点
,点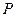 为曲线
为曲线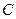 上任一点,求点
上任一点,求点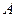 到点
到点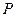 距离的最大值
距离的最大值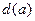 ;
;(Ⅲ)在
 的条件下,设△
的条件下,设△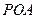 的面积为
的面积为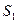 (
(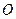 是坐标原点,
是坐标原点,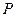 是曲线
是曲线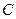 上横坐标为
上横坐标为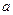 的点),以
的点),以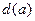 为边长的正方形的面积为
为边长的正方形的面积为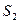 .若正数
.若正数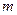 满足
满足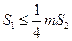 ,问
,问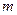 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.(Ⅰ)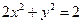 (Ⅱ)
(Ⅱ)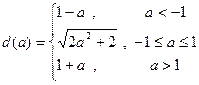 (Ⅲ)
(Ⅲ)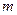 存在最小值
存在最小值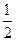
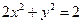 (Ⅱ)
(Ⅱ)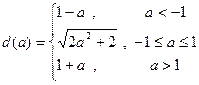 (Ⅲ)
(Ⅲ)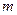 存在最小值
存在最小值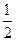
解:(Ⅰ)设圆心坐标为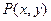 ,则动圆的半径为
,则动圆的半径为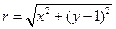 ,
,
又动圆与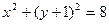 内切,所以有
内切,所以有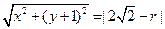 化简得
化简得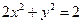
所以动圆圆心轨迹C的方程为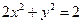 . ………………………………4分
. ………………………………4分
(Ⅱ)设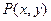 ,则
,则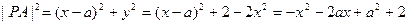
 ,令
,令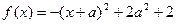 ,
,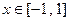 ,所以,
,所以,
当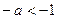 ,即
,即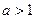 时
时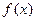 在
在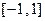 上是减函数,
上是减函数,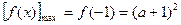 ;
;
当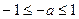 ,即
,即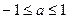 时,
时,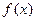 在
在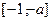 上是增函数,在
上是增函数,在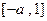 上是减函数,则
上是减函数,则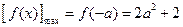 ;
;
当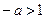 ,即
,即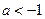 时,
时,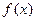 在
在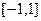 上是增函数,
上是增函数,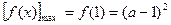 .
.
所以,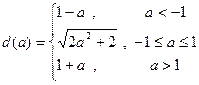 .…………………………………………9分
.…………………………………………9分
(Ⅲ)当 时,
时,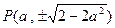 ,于是
,于是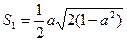 ,
, ,
,
若正数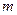 满足条件,则
满足条件,则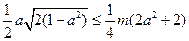 ,即
,即 ,
,
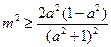 ,令
,令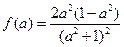 ,设
,设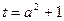 ,则
,则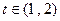 ,
,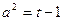 ,
,
于是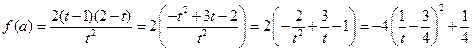 ,
,
所以,当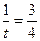 ,即
,即 时,
时,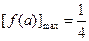 ,
,
即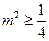 ,
,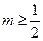 .所以,
.所以,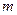 存在最小值
存在最小值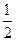 .………………………………14分
.………………………………14分
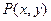 ,则动圆的半径为
,则动圆的半径为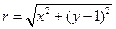 ,
,又动圆与
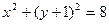 内切,所以有
内切,所以有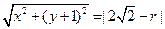 化简得
化简得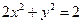
所以动圆圆心轨迹C的方程为
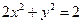 . ………………………………4分
. ………………………………4分(Ⅱ)设
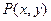 ,则
,则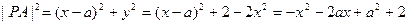
 ,令
,令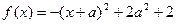 ,
,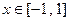 ,所以,
,所以,当
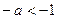 ,即
,即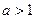 时
时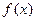 在
在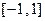 上是减函数,
上是减函数,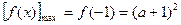 ;
;当
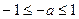 ,即
,即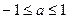 时,
时,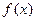 在
在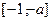 上是增函数,在
上是增函数,在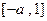 上是减函数,则
上是减函数,则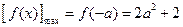 ;
;当
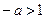 ,即
,即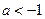 时,
时,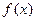 在
在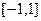 上是增函数,
上是增函数,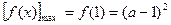 .
.所以,
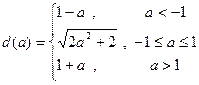 .…………………………………………9分
.…………………………………………9分(Ⅲ)当
 时,
时,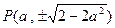 ,于是
,于是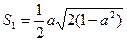 ,
, ,
,若正数
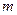 满足条件,则
满足条件,则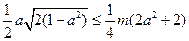 ,即
,即 ,
,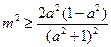 ,令
,令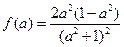 ,设
,设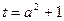 ,则
,则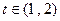 ,
,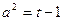 ,
,于是
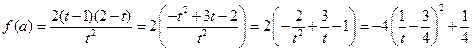 ,
,所以,当
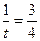 ,即
,即 时,
时,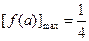 ,
,即
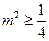 ,
,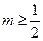 .所以,
.所以,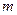 存在最小值
存在最小值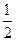 .………………………………14分
.………………………………14分
练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 =
= ,设点P的轨迹为曲线C,定点为M(4
,设点P的轨迹为曲线C,定点为M(4 ,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面
,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面 最大值.
最大值. 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 轴,若
轴,若 为双曲线的一条斜率大于0的渐近线,则
为双曲线的一条斜率大于0的渐近线,则



 且与直线
且与直线 相切.
相切. 与轨迹E交于点A、B,M是线段AB的中点,过M作
与轨迹E交于点A、B,M是线段AB的中点,过M作 轴的垂线交轨迹E于N.
轴的垂线交轨迹E于N. 与AB平行;
与AB平行; ,使
,使 ?若存在,求
?若存在,求 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线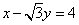 相切.
相切. 轴相交于
轴相交于 两点,圆内的动点
两点,圆内的动点 使
使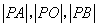 成等比数列,求
成等比数列,求 的取值范围
的取值范围 和
和 的距离之和为4的点M的轨迹是 ( )
的距离之和为4的点M的轨迹是 ( ) 、
、 ,动点
,动点 ,则点
,则点 的轨迹是 ( )
的轨迹是 ( ) 圆
圆  椭圆
椭圆  双曲线
双曲线  抛物线
抛物线 是三角形的一个内角,且
是三角形的一个内角,且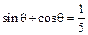 ,则方程
,则方程 所表示的曲线是( )
所表示的曲线是( ) 轴上的椭圆
轴上的椭圆 轴上的椭圆
轴上的椭圆 平行的抛物线
平行的抛物线 的切线方程是
的切线方程是


