题目内容
(本小题满分15分)已知O为坐标原点,点A、B分别在x轴,y轴上运动,且|AB|=8,动点P满足 =
= ,设点P的轨迹为曲线C,定点为M(4
,设点P的轨迹为曲线C,定点为M(4 ,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面
,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面 积的
积的 最大值.
最大值.
 =
= ,设点P的轨迹为曲线C,定点为M(4
,设点P的轨迹为曲线C,定点为M(4 ,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面
,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面 积的
积的 最大值.
最大值.(1) +=1.
(2)△OPQ的面积最大值为.
(2)△OPQ的面积最大值为.
(1)设A(a,0),B(0,b),P(x,y),
则 =(x-a,y),
=(x-a,y), =(-x,b-y),
=(-x,b-y),
 ∵
∵ =
= ,∴∴a=x
,∴∴a=x ,b=y.
,b=y.
又|AB|==8,∴+=1.
∴曲线C的方程为+=1.
(2)由(1)可知,M(4,0)为椭圆+=1的右焦点,
设直线PM方程为x=my+4,由消去x得
(9m2+25)y2+72my-81=0,
∴|yP-yQ|=
=. ∴S△OPQ=|OM||yP- yQ|=2×
yQ|=2×
===≤=,
当=,
即m=±时,△OPQ的面积取得最大值为,此时直线方程为3x±y-12=0.
则
 =(x-a,y),
=(x-a,y), =(-x,b-y),
=(-x,b-y), ∵
∵ =
= ,∴∴a=x
,∴∴a=x ,b=y.
,b=y.又|AB|==8,∴+=1.
∴曲线C的方程为+=1.
(2)由(1)可知,M(4,0)为椭圆+=1的右焦点,
设直线PM方程为x=my+4,由消去x得
(9m2+25)y2+72my-81=0,
∴|yP-yQ|=
=. ∴S△OPQ=|OM||yP-
 yQ|=2×
yQ|=2×===≤=,
当=,
即m=±时,△OPQ的面积取得最大值为,此时直线方程为3x±y-12=0.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”. .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”. 

 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.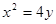 的准线方程为( )
的准线方程为( )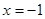
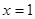
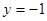
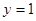
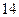 分)
分)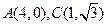 ,点M是OA的中点,点P在线段BC上运动(包括端点),如图
,点M是OA的中点,点P在线段BC上运动(包括端点),如图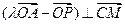 ?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。
?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。
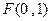 ,一动圆过点
,一动圆过点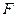 且与圆
且与圆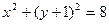 内切.
内切.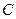 的方程;
的方程;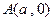 ,点
,点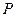 为曲线
为曲线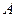 到点
到点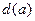 ;
; 的条件下,设△
的条件下,设△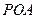 的面积为
的面积为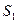 (
(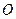 是坐标原点,
是坐标原点,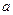 的点),以
的点),以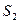 .若正数
.若正数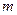 满足
满足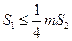 ,问
,问 ,且右顶点为
,且右顶点为 的椭圆方程;
的椭圆方程; ,焦距为10的双曲
,焦距为10的双曲 线方程。
线方程。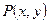 (
( )到定点
)到定点 的距离与到
的距离与到 轴的距离之差为
轴的距离之差为 .
. 的轨迹
的轨迹 的方程;
的方程; ,
, 为
为 ,求证:直线
,求证:直线 必过一定
必过一定 x, ③y=2,④y=2x+1,其中为“B型直线”的是 .(填上所有正确结论的序号)
x, ③y=2,④y=2x+1,其中为“B型直线”的是 .(填上所有正确结论的序号) 的距离比它到直线
的距离比它到直线 的距离小2,则点P的轨迹方程是 .
的距离小2,则点P的轨迹方程是 .