题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() .
.
【解析】分析:第一问将参数方程消参,求得其普通方程,对于曲线![]() ,将方程两边同时乘以
,将方程两边同时乘以![]() ,再结合极坐标与直角坐标之间的转换关系,求得极坐标方程,第二问将直线的参数方程写出=成标准形式,代入曲线方程,整理,利用韦达定理求得两根和与两根积,结合直线出参数方程中参数的几何意义求得结果.
,再结合极坐标与直角坐标之间的转换关系,求得极坐标方程,第二问将直线的参数方程写出=成标准形式,代入曲线方程,整理,利用韦达定理求得两根和与两根积,结合直线出参数方程中参数的几何意义求得结果.
详解:(1)由![]() (
(![]() 为参数),
为参数),
可得![]() 的普通方程为
的普通方程为![]() ,
,
又![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,
,
所以![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)![]() 的参数方程可化为
的参数方程可化为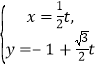 (
(![]() 为参数),
为参数),
代入![]() 得:
得:![]() ,
,
设![]() ,
,![]() 对应的直线
对应的直线![]() 的参数分别为
的参数分别为![]() ,
,![]() ,
,
![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以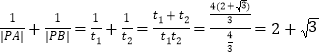 .
.

 学习实践园地系列答案
学习实践园地系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】通过随机询问100性别不同的大学生是否爱好某项运动,得到如下2×2列联表:
男 | 女 | 总计 | |
爱好 | 40 | ||
不爱好 | 25 | ||
总计 | 45 | 100 |
(1)将题中的2×2列联表补充完整;
(2)能否有99%的把握认为断爱好该项运动与性别有关?请说明理由;
附:K2= ![]() ,
,
p(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
(3)利用分层抽样的方法从以上爱好该项运动的大学生中抽取6人组建了“运动达人社”,现从“运动达人设”中选派3人参加某项校际挑战赛,记选出3人中的女大学生人数为X,求X的分布列和数学期望.

