题目内容
【题目】已知函数![]() 在
在![]() 与
与![]() 时都取得极值.
时都取得极值.
(1)求![]() 的值与函数
的值与函数![]() 的单调区间;
的单调区间;
(2)若对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】解:(1)![]() ……………………2分
……………………2分
由![]() ,
,
![]() ……………………3分
……………………3分
得![]() ……………………5分
……………………5分
(2)![]() ,
,
当![]() 时,
时,![]() 为极大值,……………………6分
为极大值,……………………6分
而![]() ,则
,则![]() 为最大值,……………………8分
为最大值,……………………8分
要使![]()
恒成立,则只需要![]() ,……………………10分
,……………………10分
得![]() ……………………12分
……………………12分
【解析】
(1)求出f![]() (x),由题意得f
(x),由题意得f![]() (
(![]() )=0且f
)=0且f![]() (1)=0联立解得
(1)=0联立解得![]() 与b的值,然后把
与b的值,然后把![]() 、b的值代入求得f(x)及f
、b的值代入求得f(x)及f![]() (x),讨论导函数的正负得到函数的增减区间;
(x),讨论导函数的正负得到函数的增减区间;
(2)根据(1)函数的单调性,由于x∈[﹣1,2]恒成立求出函数的最大值为f(2),代入求出最大值,然后令f(2)<c2列出不等式,求出c的范围即可.
(1)![]() ,f
,f![]() (x)=3x2+2ax+b
(x)=3x2+2ax+b
由 解得,
解得,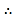
f![]() (x)=3x2﹣x﹣2=(3x+2)(x﹣1),函数f(x)的单调区间如下表:
(x)=3x2﹣x﹣2=(3x+2)(x﹣1),函数f(x)的单调区间如下表:
x | (﹣∞, |
| ( | 1 | (1,+∞) |
f | + | 0 | ﹣ | 0 | + |
f(x) |
| 极大值 |
| 极小值 |
|
所以函数f(x)的递增区间是(﹣∞,![]() )和(1,+∞),递减区间是(
)和(1,+∞),递减区间是(![]() ,1).
,1).
(2)因为![]() ,根据(1)函数f(x)的单调性,
,根据(1)函数f(x)的单调性,
得f(x)在(﹣1,![]() )上递增,在(
)上递增,在(![]() ,1)上递减,在(1,2)上递增,
,1)上递减,在(1,2)上递增,
所以当x![]() 时,f(x)
时,f(x)![]()
![]() 为极大值,而f(2)=
为极大值,而f(2)=![]() ,所以f(2)=2+c为最大值.
,所以f(2)=2+c为最大值.
要使f(x)<![]() 对x∈[﹣1,2]恒成立,须且只需
对x∈[﹣1,2]恒成立,须且只需![]() >f(2)=2+c.
>f(2)=2+c.
解得c<﹣1或c>2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目