题目内容
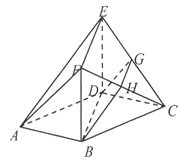
【题目】已知平面
与平面
、平面
都相交，则这三个平面可能的交线有________条.
【答案】1条、2条或3条
【解析】
分平面β与γ平行和不平行进行讨论，并且以棱柱或棱锥的侧面为例进行研究，即可得到此三个平面的交线条数可能是1条、2条或3条．
①若平面β∥平面γ，平面α与平面β，γ都相交，则它们有2条交线，且这2条交线互相平行；
②若平面β∩平面γ＝a，平面α是经过直线a的平面，则三个平面只有一条交线，即直线a；
③若平面β∩平面γ＝a，平面α与平面β，γ都相交，但交线与直线a不重合，则它们有3条交线，
例如棱柱或棱锥的三个侧面相交于三条直线，即三条侧棱
综上所述，这三个平面的交线的条数可能是1条、2条或3条，
故答案为：1条、2条或3条．
【题目】某小区为了调查居民的生活水平，随机从小区住户中抽取
个家庭，得到数据如下：
家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x（千元） | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y（千元） | 4 | 5 | 6 | 8 | 8 | 11 |
参考公式：回归直线的方程是：
，其中，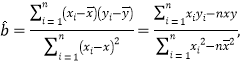
.
（1）据题中数据，求月支出
（千元）关于月收入
（千元）的线性回归方程（保留一位小数）；
（2）从这个家庭中随机抽取
个，求月支出都少于
万元的概率.
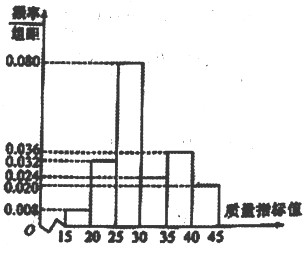
【题目】上饶市委、市政府在上饶召开上饶市全面展开新能源工程动员大会，会议动员各方力量，迅速全面展开新能源工程工作．某企业响应号召，对现有设备进行改造，为了分析设备改造前后的效果，现从设备改造前后生产的大量产品中各抽取了200件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内的产品视为合格品，否则为不合格品．图1是设备改造前的样本的频率分布直方图，表1是设备改造后的样本的频数分布表．
（1）完成
列联表，并判断是否有
的把握认为该企业生产的这种产品的质量指标值与设备改造有关；
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
（2）根据图1和表1提供的数据，试从产品合格率的角度对改造前后设备的优劣进行比较；
（3）根据市场调查，设备改造后，每生产一件合格品企业可获利200元，一件不合格品亏损150元，用频率估计概率，则生产1000件产品企业大约能获利多少元？
附：
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
．
