题目内容
5.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,|$\overrightarrow{a}$|=1,且对任意实数x,不等式|x$\overrightarrow{a}$+2$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|恒成立,则|$\overrightarrow{b}$|的取值范围是( )| A. | [$\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,+∞) | C. | [1,+∞) | D. | (1,+∞) |
分析 由题意可得x2+2|$\overrightarrow{b}$|x+(|3${\overrightarrow{b}}^{2}$-|$\overrightarrow{b}$|-1)≥0恒成立,根据△≤0,求得|$\overrightarrow{b}$|的范围.
解答 解:由题意可得x2•${\overrightarrow{a}}^{2}$+4x•$\overrightarrow{a}•\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$≥${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$ 恒成立,
化简可得x2+2|$\overrightarrow{b}$|x+(|3${\overrightarrow{b}}^{2}$-|$\overrightarrow{b}$|-1)≥0恒成立,∴△=4${|\overrightarrow{b}|}^{2}$-4(|3${\overrightarrow{b}}^{2}$-|$\overrightarrow{b}$|-1)≤0.
化简可得(2|$\overrightarrow{b}$|+1)(|$\overrightarrow{b}$|-1)≥0,求得|$\overrightarrow{b}$|≥1,
故选:C.
点评 本题主要考查两个向量的数量积的定义,二次函数的性质,函数的恒成立问题,属于基础题.

练习册系列答案
相关题目
15.△ABC外接圆的圆心O,半径为1,若$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AO}$,且|$\overrightarrow{AC}$|=|$\overrightarrow{AO}$|,则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{3}{2}$ |
16.已知函数y=f(x)是定义域为R的奇函数.当x≥0时f(x)=$\left\{{\begin{array}{l}{{x^2},0≤x≤1}\\{f(x-1)+1,x>1}\end{array}}\right.$.若恰有5个不同的实数x1,x2,…,x5,使得f(x)=mx成立,则实数m的值为( )
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | 3-2$\sqrt{2}$ |
5.正四面体ABCD中,M,N分别是棱BC和棱AC的中点,则异面直线AM和DN所成的角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 0 |
3.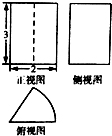 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )| A. | 2π | B. | π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |